Bài 36.10, 36.11 trang 109 SBT Vật Lí 12

36.10

Cho ba hạt nhân \(X,Y\) và \(Z\) có số nuclôn tương ứng là \({A_X},{A_Y}\) và \({A_Z}\) với \({A_X} = 2{A_Y} = 0,5{A_Z}.\) Biết năng lượng liên kết riêng của từng hạt nhân tương ứng là \(\Delta {E_X},\Delta {E_Y}\) và \(\Delta {E_Z}\) với \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y}.\) Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là:

A. \(Y,X,Z.\)                          B. \(Y,Z,X.\)

C. \(X,Y,Z.\)                          D. \(Z,X,Y.\)

Phương pháp giải:

Sử dụng lí thuyết hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững

Sử dụng công thức tính năng lượng liên kết riêng: \(\sigma  = \dfrac{{\Delta E}}{A} = \dfrac{{\Delta m{c^2}}}{A}\)

Lời giải chi tiết:

Ta  có công thức tính năng lượng liên kết riêng \(\sigma  = \dfrac{{\Delta E}}{A} = \dfrac{{\Delta m{c^2}}}{A}\)

+ Ta có \({A_X} = 2{A_Y} = 0,5{A_Z}\\ \Rightarrow {A_Z} > {A_X} > {A_Y}\)

+\(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y}.\)

Vậy \({\sigma _Z} < {\sigma _X} < {\sigma _Y}\)  nên thứ tự tính bền vững giảm dần là: \(Y,X,Z\)

Chọn A

36.11

Bắn một prôtôn vào hạt nhân \({}_3^7Li\) đứng yên. Phản ứng tạo ra hai hạt nhân \(X\) giống nhau bay ra với cùng tốc độ và theo phương hợp với phương tới của prôtôn các góc bằng nhau là \({60^o}.\) Lấy khối lượng của mỗi hạt nhân, tính theo đơn vị \(u,\) bằng số khối của nó. Tỉ số giữa tốc độ của prôtôn và tốc độ của hạt nhân \(X\) là

A. \(4.\)                                            B. \(\dfrac{1}{2}.\)

C. \(2.\)                                            D. \(\dfrac{1}{4}.\)

Phương pháp giải:

Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân

Lời giải chi tiết:

Phương trình phản ứng hạt nhân: \(_1^1p + _3^7Li \to X + X\)

Vậy \(X\) là \(_2^4He\)

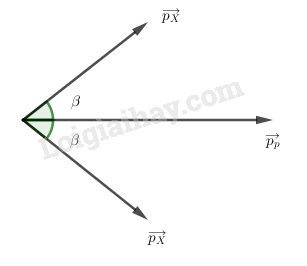
Bảo toàn động lượng: \(\overrightarrow {{p_p}}  = \overrightarrow {2{p_X}} \)

Chiếu lên phương của \(\overrightarrow {{p_p}} \) :

\(\begin{array}{l}{p_p} = 2{p_X}\cos \beta \\ \Leftrightarrow {m_p}{v_p} = 2{m_X}{v_X}\cos \beta \\ \Rightarrow \dfrac{{{v_p}}}{{{v_X}}} = \dfrac{{2{m_X}\cos \beta }}{{{m_p}}} \\= \dfrac{{2.4.\cos {{60}^0}}}{1} = 4\end{array}\)

Chọn A