Bài 3.6 trang 130 SBT hình học 11

Đề bài

Trên mặt phẳng \(\displaystyle \left( \alpha  \right)\) cho hình bình hành \(\displaystyle {A_1}{B_1}{C_1}{D_1}\). Về một phía đối với mặt phẳng \(\displaystyle \left( \alpha  \right)\) ta dựng hình bình hành \(\displaystyle {A_2}{B_2}{C_2}{D_2}\). Trên các đoạn \(\displaystyle {A_1}{A_2},{B_1}{B_2},{C_1}{C_2},{D_1}{D_2}\) ta lần lượt lấy các điểm \(A, B, C, D\) sao cho

\(\displaystyle {{A{A_1}} \over {A{A_2}}} = {{B{B_1}} \over {B{B_2}}} = {{C{C_1}} \over {C{C_2}}} = {{D{D_1}} \over {D{D_2}}} = 3\) 

Chứng minh rằng tứ giác \(\displaystyle ABCD\) là hình bình hành.

Lời giải chi tiết

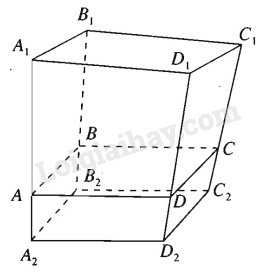
Lấy điểm \(O\) cố định rồi đặt \(\overrightarrow {O{A_1}}  = \overrightarrow {{a_1}} ,\,\,\overrightarrow {O{B_1}}  = \overrightarrow {{b_1}} ,\,\,\overrightarrow {O{C_1}}  = \overrightarrow {{c_1}} ,\,\,\overrightarrow {O{D_1}}  = \overrightarrow {{d_1}} \). Điều kiện cần và đủ để tứ giác \({A_1}{B_1}{C_1}{D_1}\) là hình bình hành là \(\overrightarrow {{a_1}}  + \overrightarrow {{c_1}}  = \overrightarrow {{b_1}}  + \overrightarrow {{d_1}} \) ( theo bài tập 3.2)   (1)

Đặt \(\overrightarrow {O{A_2}}  = \overrightarrow {{a_2}} ,\overrightarrow {O{B_2}}  = \overrightarrow {{b_2}},\) \(\overrightarrow {O{C_2}}  = \overrightarrow {{c_2}} ,\overrightarrow {O{D_2}}  = \overrightarrow {{d_2}} \).

Điều kiện cần và đủ để tứ giác \({A_2}{B_2}{C_2}{D_2}\) là hình bình hành là \(\overrightarrow {{a_2}}  + \overrightarrow {{c_2}}  = \overrightarrow {{b_2}}  + \overrightarrow {{d_2}} \)     (2)

Đặt \(\overrightarrow {OA}  = \overrightarrow a ,\,\,\overrightarrow {OB}  = \overrightarrow b ,\,\,\overrightarrow {OC}  = \overrightarrow c ,\,\,\overrightarrow {OD}  = \overrightarrow d \).

Ta có \({{A{A_1}} \over {A{A_2}}} = 3 \Rightarrow \overrightarrow {A{A_1}}  =  - 3\overrightarrow {A{A_2}} \)

\(\eqalign{
& \Leftrightarrow \overrightarrow {O{A_1}} - \overrightarrow {OA} = 3\left( {\overrightarrow {O{A_2}} - \overrightarrow {OA} } \right) \cr 
& \Leftrightarrow \overrightarrow {{a_1}} - \overrightarrow a = - 3\left( {\overrightarrow {{a_2}} - \overrightarrow a } \right) \cr 
& \Leftrightarrow \overrightarrow a = {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) \cr} \)

Tương tự: \(\overrightarrow b  = {1 \over 4}\left( {\overrightarrow {{b_1}}  + 3\overrightarrow {{b_2}} } \right)\),

\(\overrightarrow c  = {1 \over 4}\left( {\overrightarrow {{c_1}}  + 3\overrightarrow {{c_2}} } \right),\overrightarrow {\,\,d}  = {1 \over 4}\left( {\overrightarrow {{d_1}}  + 3\overrightarrow {{d_2}} } \right)\).

Ta có: \(\overrightarrow a  + \overrightarrow c  = {1 \over 4}\left( {\overrightarrow {{a_1}}  + 3\overrightarrow {{a_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{c_1}}  + 3\overrightarrow {{c_2}} } \right)\)

\(= {1 \over 4}\left( {\overrightarrow {{a_1}}  + \overrightarrow {{c_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{a_2}}  + \overrightarrow {{c_2}} } \right)\)

Và:

\(\eqalign{
& \overrightarrow b + \overrightarrow d = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right) \cr 
& = {1 \over 4}\left( {\overrightarrow {{b_1}} + \overrightarrow {{d_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{b_2}} + \overrightarrow {{d_2}} } \right) \cr}\)

Từ (1) và (2) ta có \(\overrightarrow {{a_1}}  + \overrightarrow {{c_1}}  = \overrightarrow {{b_1}}  + \overrightarrow {{d_1}} \) và \(\overrightarrow {{a_2}}  + \overrightarrow {{c_2}}  = \overrightarrow {{b_2}}  + \overrightarrow {{d_2}} \) nên suy ra :

\(\overrightarrow a  + \overrightarrow b  + \overrightarrow c  + \overrightarrow d  \Leftrightarrow \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB}  + \overrightarrow {O{\rm{D}}} \)

⟺ tứ giác \(ABCD\) là hình bình hành.