Bài 3.5 trang 130 SBT hình học 11
Giải bài 3.5 trang 130 sách bài tập hình học 11. Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A...
Đề bài
Trong không gian cho hai hình bình hành \(ABCD\) và \(A’B’C’D’\) chỉ có chung nhau một điểm \(A\). Chứng minh rằng các vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) đồng phẳng.
Phương pháp giải - Xem chi tiết
Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) suy ra điều phải chứng minh.
Lời giải chi tiết
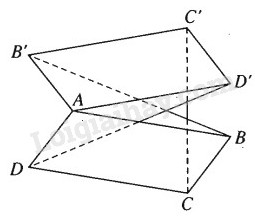
Ta có :
\(\overrightarrow {BB'} = \overrightarrow {BA} + \overrightarrow {AB'} ,\)
\(\overrightarrow {DD'} = \overrightarrow {DA} + \overrightarrow {AD'} \)
Do đó \(\overrightarrow {BB'} + \overrightarrow {DD'} \) \(= \left( {\overrightarrow {BA} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right)\)
Vì \(\overrightarrow {BA} = \overrightarrow {C{\rm{D}}} \) và \(\overrightarrow {AB'} + \overrightarrow {AD'} = \overrightarrow {AC'} \)
Nên \(\overrightarrow {BB'} + \overrightarrow {DD'} = \left( {\overrightarrow {C{\rm{D}}} + \overrightarrow {DA} } \right) + \overrightarrow {AC'} \)
Vậy \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \)
Hệ thức \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) biểu thị sự đồng phẳng của ba vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.5 trang 130 SBT hình học 11 timdapan.com"







