Bài 35 trang 141 SBT toán 7 tập 1
Giải bài 35 trang 141 sách bài tập toán 7 tập 1. Cho đường thẳng xy, các điểm B và C nằm trên xy, điểm A nằm ngoài xy...
Đề bài
Cho đường thẳng \(xy\), các điểm \(B\) và \(C\) nằm trên \(xy\), điểm \(A\) nằm ngoài \(xy.\) Dựa vào bài \(34\), hãy nêu cách vẽ đường thẳng đi qua \(A\) và song song với \(BC.\)
Phương pháp giải - Xem chi tiết
- Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
- Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
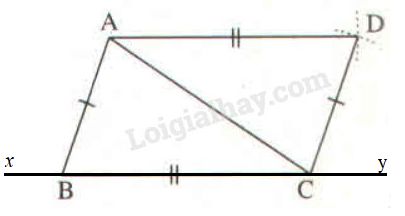
Trên đường thẳng \(xy\), các điểm \(B\) và \(C\) nằm trên \(xy\), điểm \(A\) nằm ngoài \(xy.\)
Nối \(AB.\) Trên nửa mặt phẳng bờ \(BC\) có chứa điểm \(A\) ta làm như sau:
- Vẽ cung tròn tâm \(A\) bán kính bằng \(BC.\)
- Vẽ cung tròn tâm \(C\) bán kính bằng \(AB.\)
- Hai cung tròn cắt nhau tại \(D.\)
- Kẻ đường thẳng \(AD\) ta có \(AD // xy.\)
Chứng minh:
Cung tròn tâm \(C\) bán kính bằng \( AB\); \(D\) thuộc cung tròn nên \(CD=BA\).
Cung tròn tâm \(A\) bán kính bằng \(BC\); \(D\) thuộc cung tròn nên \(AD=BC\).
Xét \(∆ABC\) và \(∆CDA\), ta có:
\(AB = CD\) (chứng minh trên)
\(AC\) cạnh chung
\(BC = AD\) (chứng minh trên)
\( \Rightarrow \Delta ABC{\rm{ }} = {\rm{ }}\Delta CDA{\rm{ }}\left( {c.c.c} \right) \)
\(\Rightarrow \widehat {ACB} = \widehat {CA{\rm{D}}}\) (hai góc tương ứng).
Vậy \(AD // BC\) (vì có cặp góc ở vị trí so le trong \( \widehat {ACB} = \widehat {CA{\rm{D}}}\)).
Hay \(AD//xy\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 35 trang 141 SBT toán 7 tập 1 timdapan.com"







