Bài 3.23 trang 150 SBT hình học 11
Giải bài 3.23 trang 150 sách bài tập hình học 11. Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD.
Đề bài
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh \(MN \bot AB\) và \(MN \bot C{\rm{D}}\). Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Phương pháp giải - Xem chi tiết
- Sử dụng tam giác bằng nhau, tính chất tam giác cân để chứng minh đường thẳng \(MN\) vuông góc với hai đường thẳng \(AB,CD\).
Lời giải chi tiết
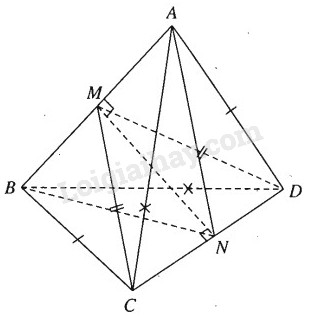
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó \(MN \bot C{\rm{D}}\) vì N là trung điểm của CD.
Tương tự ta chứng minh được NA = NB và suy ra \(MN \bot AB\).
Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.23 trang 150 SBT hình học 11 timdapan.com"







