Giải bài 3.18 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức

Đề bài

Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Một đường thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ đó suy ra tứ giác MBND là hình bình hành.

Lời giải chi tiết

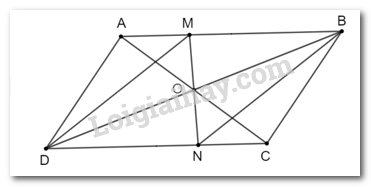
Vì ABCD là hình bình hành nên ta có:

• Hai đường chéo AC và BD cắt nhau tại O nên OA = OC, OB = OD.

• AB // CD nên AM // CN suy ra \(\widehat {OAM} = \widehat {OCN}\) (hai góc so le trong).

Xét ∆OAM và ∆OCN có:

\(\widehat {OAM} = \widehat {OCN}\) (chứng minh trên)

OA = OC (chứng minh trên)

\(\widehat {AOM} = \widehat {CON}\) (hai góc đối đỉnh)

Do đó ∆OAM = ∆OCN (g.c.g).

Suy ra AM = CN (hai cạnh tương ứng)

Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN.

Suy ra BM = DN.

Xét tứ giác MBND có:

• BM // DN (vì AB // CD)

• BM = DN (chứng minh trên)

Do đó, tứ giác MBND là hình bình hành.