Giải bài 3 trang 72 SGK Toán 10 tập 1 – Chân trời sáng tạo
Cho tam giác ABC, biết cạnh. Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Đề bài
Cho tam giác ABC, biết cạnh \(a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}.\) Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Phương pháp giải - Xem chi tiết
Áp dụng định lí sin:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Lời giải chi tiết
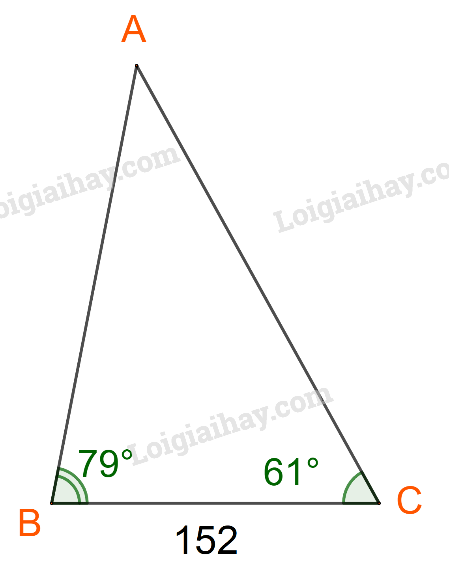
Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(a = 152;\widehat A = {180^o} - ({79^o} + {61^o}) = {40^o}\)
Áp dụng định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra:
\(\begin{array}{l}AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{152.\sin {{79}^o}}}{{\sin {{40}^o}}} \approx 232,13\\AB = c = \frac{{a.\sin C}}{{\sin A}} = \frac{{152.\sin {{61}^o}}}{{\sin {{40}^o}}} \approx 206,82\\R = \frac{a}{{\sin A}} = \frac{{152}}{{\sin {{40}^o}}} \approx 236,47\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 72 SGK Toán 10 tập 1 – Chân trời sáng tạo timdapan.com"







