Giải bài 3 trang 111 SGK Toán 7 tập 2 - Cánh diều
Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.
Đề bài
Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.
a) Chứng minh \(\widehat {CBI} > \widehat {ACI}\);
b) So sánh IB và IC.
Phương pháp giải - Xem chi tiết
a) Góc đối diện với cạnh lớn hơn thì có số đo góc lớn hơn.
b) Cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn.
Lời giải chi tiết
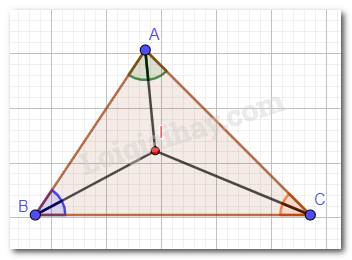
a) Ta có: AB < AC nên \(\widehat {ABC} > \widehat {ACB}\)(góc ABC đối diện với cạnh AC; góc ACB đối diện với cạnh AB).
Mà BI và CI là hai đường phân giác của góc ABC và góc ACB nên: \(\widehat {CBI} > \widehat {ACI}\)
(Vì: \(\widehat {CBI} = \dfrac{1}{2}\widehat {ABC};\widehat {ACI} = \dfrac{1}{2}\widehat {ACB}\)).
b) Ta có: \(\widehat {ACI} = \widehat {BCI}\)
Mà \(\widehat {CBI} > \widehat {ACI}\) ( câu a)
Do đó \(\widehat {CBI} > \widehat {BCI}\).
Mà IC đối diện với góc CBI; IB đối diện với góc BCI.
Vậy IC > IB (cạnh đối diện với góc lớn hơn thì có số đo độ dài lớn hơn).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 111 SGK Toán 7 tập 2 - Cánh diều timdapan.com"







