Bài 2.7 phần bài tập bổ sung trang 168 SBT toán 8 tập 1
Giải bài 2.7 phần bài tập bổ sung trang 168 sách bài tập toán 8. Cho hình bs.31, R là điểm bất kì trên QP, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó tổng diện tích của hai tam giác QSP và NRO bằng:
Đề bài
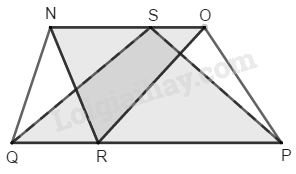
Cho hình bs.31, (\(R\) là điểm bất kì trên \(QP,\, S\) là điểm bất kì trên \(NO,\) hình thang \(NOPQ\) có diện tích \(S\)). Khi đó tổng diện tích của hai tam giác \(QSP\) và \(NRO\) bằng:
(A) \(\dfrac {1}{2}S\)
(B) \(\dfrac {1}{4}S\)
(C) \(\dfrac {3}{4}S\)
(D) \(S\)
Phương pháp giải - Xem chi tiết
Dựa vào công thức tính diện tích tam giác bằng nửa tích chiều cao và cạnh đáy tương ứng: \(S=\dfrac {1}{2}ah\)
Lời giải chi tiết
Gọi chiều cao của hình thang \(NOPQ\) là \(h\). độ dài đoạn thẳng \(NO,\, QP\) lần lượt là \(a,\,b\)
Khi đó diện tích hình thang \(NOPQ\): \(S= \dfrac {a+b}{2}.h\)
Ta có: \(S_{QSP}=\dfrac {1}{2}h.b\)
\(S_{NRO}=\dfrac {1}{2}h.a\)
Vậy tổng diện tích của hai tam giác là:
\(S_{QSP}+S_{NRO}\) \(=\dfrac {1}{2}h.b+\dfrac {1}{2}h.a\) \(=\dfrac {a+b}{2}.h\)
Vậy \(S_{QSP}+S_{NRO}=S\)
Chọn (D)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.7 phần bài tập bổ sung trang 168 SBT toán 8 tập 1 timdapan.com"







