Giải bài 26 trang 110 sách bài tập toán 9 - Cánh diều tập 1
Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC. Chứng minh: a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’); b) Hai đường tròn (O) và (O') tiếp xúc ngoài; c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’); d) AH = DE; e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Hình chiếu của H trên AB, AC lần lượt là D, E. Gọi (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC. Chứng minh:
a) Điểm D thuộc đường tròn (O) và điểm E thuộc đường tròn (O’);
b) Hai đường tròn (O) và (O') tiếp xúc ngoài;
c) AH là tiếp tuyến chung của hai đường tròn (O) và (O’);
d) AH = DE;
e) Diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Phương pháp giải - Xem chi tiết
a) Chứng minh \(OB = OD = OH = \frac{{BH}}{2}\); \(O'H = O'E = O'C = \frac{{HC}}{2}\).
b) Chứng minh \(OO' = OH + O'H\).
c) Chứng minh \(AH \bot OO'\).
d) Chứng minh ADHE là hình chữ nhật.
e) Bước 1: Chứng minh ODEO’ là hình thang vuông.
Bước 2: Biểu diễn diện tích 2 hình theo công thức.
Bước 3: Vận dụng dữ kiện \(AH = DE\), \(BC = BH + CH = 2\left( {OD + O'E} \right)\) để biến đổi.
Lời giải chi tiết
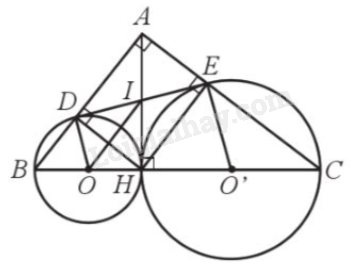
a) Do tam giác BDH vuông tại D và O là trung điểm của BH (BO và HO là bán kính đường tròn (O)) nên \(OB = OD = OH = \frac{{BH}}{2}\), do đó D thuộc đường tròn (O).
Do tam giác ECH vuông tại E và O’ là trung điểm của CH (O’H và O’C là bán kính đường tròn (O)) nên \(O'H = O'E = O'C = \frac{{HC}}{2}\), do đó E thuộc đường tròn (O’).
b) Do tam giác ABC vuông tại A có AH là đường cao, \(H \in BC\) nên H nằm giữa B và C.
Mà (O) là đường tròn đường kính HB và (O') là đường tròn đường kính HC nên H nằm giữa O và O’, do đó \(OO' = OH + O'H\), vậy đường tròn (O) và (O') tiếp xúc ngoài.
c) Ta có OH, O’H lần lượt là bán kính của (O) và (O’) , và AH vuông góc với OO’ tại H nên AH là tiếp tuyến chung của hai đường tròn (O) và (O’).
d) Do tam giác BDH vuông tại D nên \(\widehat {BDH} = 90^\circ \), do đó \(\widehat {HDA} = 90^\circ \).
Do tam giác ECH vuông tại E nên \(\widehat {ECH} = 90^\circ \), do đó \(\widehat {HEA} = 90^\circ \).
Xét tứ giác ADHE có \(\widehat {HDA} = \widehat {HEA} = \widehat {DAE} = 90^\circ \) nên ADHE là hình chữ nhật, do đó \(AH = DE\).
e) Do ADHE là hình chữ nhật nên \(IA = ID = IH = IE\).
Xét hai tam giác OID và OIH có:
\(OD = OH\);
OI chung;
\(ID = IH\)
Suy ra \(\Delta OID = \Delta OIH\) (c.c.c), do đó \(\widehat {OHI} = \widehat {ODI} = 90^\circ \), hay \(OD \bot DE\).
Xét hai tam giác OIE và O’IH có:
\(O'E = O'H\);
O’I chung;
\(IE = IH\)
Suy ra \(\Delta OIE = \Delta O'IH\)(c.c.c), do đó \(\widehat {O'HI} = \widehat {O'EI} = 90^\circ \), hay \(O'E \bot DE\).
Xét ODEO’ có \(OD \bot DE\), \(O'E \bot DE\) nên \(OD//EO'\), do đó ODEO’ là hình thang vuông và DE là đường cao.
Diện tích hình thang ODEO’ và tam giác ABC lần lượt là: \({S_1} = \frac{{DE\left( {OD + O'E} \right)}}{2};{S_2} = \frac{{AH.BC}}{2}\)
Mà \(AH = DE\), \(BC = BH + CH = 2\left( {OD + O'E} \right)\)
Suy ra \({S_1} = \frac{1}{2}{S_2}\).
Vậy diện tích tứ giác DEO’O bằng nửa diện tích tam giác ABC.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 26 trang 110 sách bài tập toán 9 - Cánh diều tập 1 timdapan.com"







