Bài 2.20 trang 41 SBT đại số 10

Đề bài

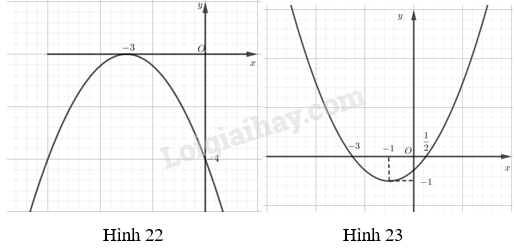
Viết phương trình của parabol \(y = a{x^2} + bx + c\) ứng với mỗi đồ thị dưới đây

Lời giải chi tiết

a) Dựa trên đồ thị (h.22) ta thấy parabol có đỉnh \(I( - 3;0)\) và đi qua điểm \((0; - 4)\)

Như vậy \(c =  - 4; - \dfrac{b}{{2a}} =  - 3 \Leftrightarrow b = 6a\).

Thay \(c =  - 4\) và \(b = 6a\) vào biểu thức

\(\Delta  = {b^2} - 4ac = 0\)\( =  > 36{a^2} + 16a = 0 \) \(=  > a =  - \dfrac{4}{9}\) (vì \(a \ne 0)\) và \(b =  - \dfrac{8}{3}\).

Vậy phương trình của parabol là \(y =  - \dfrac{4}{9}{x^2} - \dfrac{8}{3}x - 4\).

b) Dựa trên đồ thị (h.23) ta thấy parabol có đỉnh \(I( - 1; - 1)\) và đi qua điểm \(\left( {\dfrac{1}{2};0} \right)\)

Như vậy \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{1}{4}a + \dfrac{1}{2}b + c = 0}\\{ - \dfrac{b}{{2a}} =  - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{b = 2a}\\{c =  - \dfrac{5}{4}a}\end{array}} \right.\).

Thay vào biểu thức \(\Delta  = {b^2} - 4ac =  - 1 \) \(=  > 4{a^2} + 5a + 1 = 0 =  > a = \dfrac{4}{9}\) (vì \(a > 0)\) \( \Rightarrow b = \dfrac{8}{9};c = \dfrac{{ - 5}}{9}\).

\(y = \dfrac{4}{9}{x^2} + \dfrac{8}{9}x - \dfrac{5}{9}\)