Bài 21 trang 102 SBT toán 9 tập 2
Giải bài 21 trang 102 sách bài tập toán 9. Cho tam giác ABC nội tiếp trong đường tròn tâm O,...
Đề bài
Cho tam giác \(ABC\) nội tiếp trong đường tròn tâm \(O,\) biết \(\widehat A = {32^0}\), \(\widehat B = {84^0}\). Lấy các điểm \(D, E, F\) thuộc đường tròn tâm \(O\) sao cho \(AD = AB,\) \(BE = BC,\) \(CF = CA.\) Hãy tính các góc của tam giác \(DEF.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải chi tiết
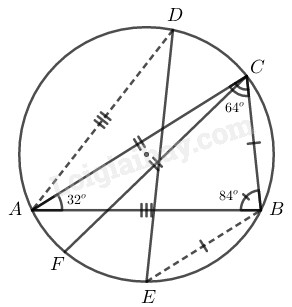
Xét đường tròn \((O)\) có:
\(\widehat A =\displaystyle {1 \over 2} sđ \overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{BC}\) \( = 2\widehat A = {2.32^o} = {64^o}\)
Ta có: \(BC = BE \;\;(gt)\)
\( \Rightarrow sđ \overparen{BC}\)\( = sđ \overparen{BE}= 64^o\)
Mà \(\widehat B = \displaystyle {1 \over 2} sđ \overparen{AC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AC}\) \( = 2\widehat B = {2.84^o} = {168^o}\)
Lại có: \(AC = CF \;\;(gt)\)
\( \Rightarrow sđ \overparen{CF}\) \(= sđ \overparen{AC}= 168^o\)
\( sđ \overparen{AC} + sđ \overparen{AF} + sđ \overparen{CF}\)\( = 360^o\)
\( \Rightarrow sđ \overparen{AF}\) \( = {360^o} - sđ \overparen{AC} - sđ \overparen{CF}\)\( = 360^o – 168^o. 2 = 24^o\)
Trong \(∆ABC\) ta có: \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat A + \widehat B} \right)\)
\( = {180^0} - \left( {{{32}^o} + {{84}^o}} \right) = {64^o}\)
Mà \( \widehat {ACB} = \displaystyle {1 \over 2} sđ \overparen{AB}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{AB} = 2\widehat {ACB} = {2.64^o} = {128^o}\)
Lại có \(AD = AB\;\; (gt)\)
\( \Rightarrow sđ \overparen{AD} = sđ \overparen{AB} = 128^o\)
Ta có: \(\widehat {FED} = \displaystyle {1 \over 2} sđ \overparen{DF}\) \( =\displaystyle {1 \over 2} ( sđ \overparen{AD} + sđ \overparen{AF}\))
\(= \displaystyle{1 \over 2}.\left( {{{128}^o} + {{24}^o}} \right) = {76^o}\)
\(\widehat {EDF} = \displaystyle{1 \over 2} sđ \overparen{EF}\) \(=\displaystyle {1 \over 2} ( sđ \overparen{AB} - sđ \overparen{AF} - sđ \overparen{BE})\)
\(= \displaystyle{1 \over 2}.\left( {{{128}^o} - {{24}^o} - {{64}^o}} \right) = {20^o}\)
\(\widehat {DFE} = {180^o} - \left( {\widehat {FED} + \widehat {EDF}} \right)\)
\(= {180^0} - \left( {{{76}^o} + {{20}^o}} \right) = {84^o}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 21 trang 102 SBT toán 9 tập 2 timdapan.com"







