Bài 15 trang 102 SBT toán 9 tập 2
Giải bài 15 trang 102 sách bài tập toán 9. Cho đường tròn tâm O, bán kính 1,5cm. Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ.
Đề bài
Cho đường tròn tâm \(O\), bán kính \(1,5cm\). Hãy vẽ hình vuông \(ABCD\) có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ.
Phương pháp giải - Xem chi tiết
+) Vẽ hình: dùng thước thẳng và compa để vẽ hình
+) Chứng minh: Sử dụng dấu hiệu nhận biết hình bình hành và hình vuông
Dấu hiệu nhận biết hình bình hành: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Dấu hiệu nhận biết hình vuông: Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
Lời giải chi tiết
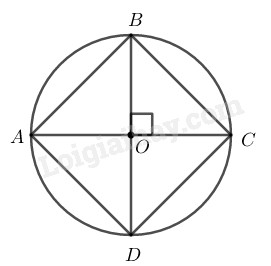
Cách vẽ:
- Vẽ đường tròn \((O; 1,5cm)\)
- Vẽ 2 đường kính \(AC\) và \(BD\) vuông góc với nhau.
- Nối \(AB, BC, CD, DA\) ta có tứ giác \(ABCD\) là hình vuông có \(4\) đỉnh nằm trên cung tròn \((O; 1,5cm)\).
Chứng minh:
Theo cách vẽ ta có: \(OA = OC=R, OB = OD=R\) nên tứ giác \(ABCD\) là hình bình hành
Lại có: \(AC = BD=2R\) nên hình bình hành \(ABCD\) là hình chữ nhật.
Mặt khác: \(BD \bot AC\) nên hình chữ nhật \(ABCD\) là hình vuông.
Vậy tứ giác \(ABCD\) là hình vuông.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 15 trang 102 SBT toán 9 tập 2 timdapan.com"







