Bài 2 trang 148 Vở bài tập toán 8 tập 2

Đề bài

Chứng minh rằng: 

\(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\)

Lời giải chi tiết

Xét hiệu hai vế:  

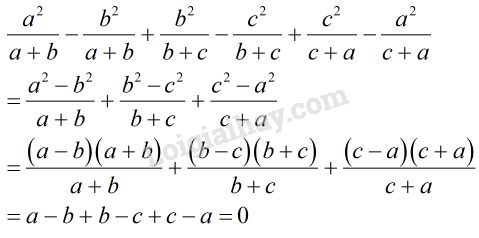
\(\Rightarrow\) \(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}} = \dfrac{{{b^2}}}{{a + b}} \)\(\,+ \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\) 

Lưu ý:

Có thể giải bằng cách biến đổi từ vế trái sang vế phải như sau:

\(\dfrac{{{a^2}}}{{a + b}} + \dfrac{{{b^2}}}{{b + c}} + \dfrac{{{c^2}}}{{c + a}}\)

\( = \dfrac{{{a^2} - {b^2} + {b^2}}}{{a + b}} + \dfrac{{{b^2} - {c^2} + {c^2}}}{{b + c}}\)\( + \dfrac{{{c^2} - {a^2} + {a^2}}}{{c + a}}\)

\( = \dfrac{{\left( {a + b} \right)\left( {a - b} \right) + {b^2}}}{{a + b}} + \dfrac{{\left( {b + c} \right)\left( {b - c} \right) + {c^2}}}{{b + c}} \)\(+ \dfrac{{\left( {c + a} \right)\left( {c - a} \right) + {a^2}}}{{c + a}}\)

\( = a - b + \dfrac{{{b^2}}}{{a + b}} + b - c\)\( + \dfrac{{{c^2}}}{{b + c}} + c - a + \dfrac{{{a^2}}}{{c + a}}\)

\( = \dfrac{{{b^2}}}{{a + b}} + \dfrac{{{c^2}}}{{b + c}} + \dfrac{{{a^2}}}{{c + a}}\)