Bài 17 trang 87 SBT toán 8 tập 2
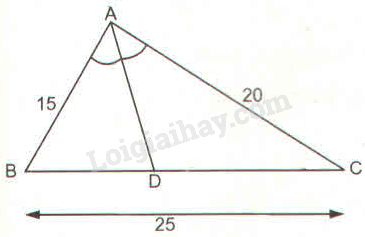
Giải bài 17 trang 87 sách bài tập toán 8. Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D (h.14)
Đề bài
Tam giác \(ABC\) có \(AB = 15cm, AC = 20cm,\) \( BC = 25cm.\) Đường phân giác góc \(BAC\) cắt cạnh \(BC\) tại \(D\) (h.14)
a) Tính độ dài đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích của hai tam giác \(ABD\) và \(ACD.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Tính chất: \(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
Lời giải chi tiết
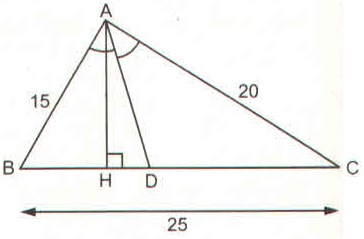
a) Áp dụng tính chất đường phân giác vào \(\Delta ABC\), đường phân giác \(AD\) ta có:
\(\displaystyle {{DB} \over {DC}} = {{AB} \over {AC}}\)
\(\displaystyle \Rightarrow {{DB} \over {DC}} = {{15} \over {20}}=\dfrac{3}{4}\)
Ta có:
\(\displaystyle {{DB} \over {DC}} = \dfrac{3}{4}\)
\( \displaystyle \Rightarrow {{DB} \over {DB + DC}} = \dfrac{3}{{3 + 4}}\)
\(\displaystyle \Rightarrow {{DB} \over {BC}} = \dfrac{3}{7}\)
\( \displaystyle \Rightarrow DB = \dfrac{3}{7}.BC = \dfrac{3}{7}.25 = {{75} \over 7}\) (cm)
b) Kẻ \(AH ⊥ BC\)
Ta có: \(\displaystyle {S_{ABD}} = {1 \over 2}AH.BD;\) \(\displaystyle {S_{ADC}} = {1 \over 2}AH.DC\)
\(\Rightarrow\displaystyle {{{S_{ABD}}} \over {{S_{ADC}}}} = {\displaystyle{{1 \over 2}AH.BD} \over {\displaystyle{1 \over 2}AH.DC}} = {{BD} \over {DC}}\)
Mà \(\displaystyle {{DB} \over {DC}} = {{15} \over {20}} = {3 \over 4}\) (chứng minh trên )
Vậy \(\displaystyle {{{S_{ABD}}} \over {{S_{ADC}}}} = {3 \over 4}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 17 trang 87 SBT toán 8 tập 2 timdapan.com"







