Bài 1.13 trang 21 SBT hình học 10
Giải bài 1.13 trang 21 sách bài tập hình học 10. Cho tam giác ABC có trung tuyến AM...
Đề bài
Cho tam giác \(ABC\) có trung tuyến \(AM\). Trên cạnh \(AC\) lấy hai điểm \(E\) và \(F\) sao cho \(AE = EF= FC\); \(BE\) cắt \(AM \) tại \(N\). Chứng minh \(\overrightarrow {NA} \) và \(\overrightarrow {NM} \) là hai vec tơ đối nhau.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức hình học đã biết chứng minh \(N\) là trung điểm của \(AM\).
Lời giải chi tiết
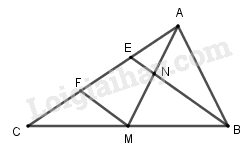
\(FM // BE \) vì \(FM\) là đường trung bình của tam giác \(CEB\).
Ta có \(EA = EF\). Vậy \( EN\) là đường trung bình của tam giác \(AFM\).
Do đó \(N\) là trung điểm của \(AM\) và \(\overrightarrow {NA} = - \overrightarrow {NM} \).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.13 trang 21 SBT hình học 10 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.13 trang 21 SBT hình học 10 timdapan.com"







