Bài 11 trang 90 Vở bài tập toán 9 tập 1
Giải bài 11 trang 90 VBT toán 9 tập 1. Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2 m...
Đề bài
Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2 m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác củ góc A.
Phương pháp giải - Xem chi tiết
- Dùng định lí Pi-ta-go tính độ dài cạnh chưa biết của tam giác vuông.
- Áp dụng công thức tính tỉ số lượng giác của các góc trong tam giác vuông :
\(\sin \alpha = \dfrac{{cạnh\,\,đối}}{{cạnh\,\,huyền}}\) ;
\(\cos \alpha = \dfrac{{cạnh\,\,kề}}{{cạnh\,\,huyền}}\) ;
\(\tan \alpha = \dfrac{{cạnh\,\,đối}}{{cạnh\,\,kề}}\);
\(\cot \alpha = \dfrac{{cạnh\,\,kề}}{{cạnh\,\,đối}}\)
- Vận dụng kiến thức : Cho hai góc \(\alpha \) và \(\beta \) phụ nhau \(\left( {\alpha + \beta = {{90}^o}} \right)\).
Ta có: \(\sin \alpha = \cos \beta ;\,\,\cos \alpha = \sin \beta ;\)\(\,\tan \alpha = \cot \beta ;\,\,\cot \alpha = \tan \beta \)
Lời giải chi tiết
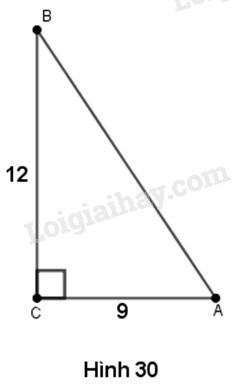
\(AC = 0,9m = 9dm;\)\(BC = 1,2m = 12dm\)
Trong tam giác vuông \(ABC\), theo định lí Pi-ta-go, ta có :
\(AB = \sqrt {{{12}^2} + {9^2}} = \sqrt {225} = 15\left( {dm} \right).\)
Do đó:
\(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{9}{{15}} = \dfrac{3}{5},\) \(\cos B = \dfrac{{BC}}{{AB}} = \dfrac{{12}}{{15}} = \dfrac{4}{5},\)
\(\tan B = \dfrac{{AC}}{{BC}} = \dfrac{9}{{12}} = \dfrac{3}{4},\) \(\cot B = \dfrac{{BC}}{{AC}} = \dfrac{{12}}{9} = \dfrac{4}{3}\)
Vì \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau nên :
\(\sin A = \cos B = \dfrac{4}{5},\) \(\cos A = \sin B = \dfrac{3}{5},\)
\(\tan A = \cot B = \dfrac{4}{5},\) \(\cot A = \tan B = \dfrac{3}{4}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 11 trang 90 Vở bài tập toán 9 tập 1 timdapan.com"







