Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

I. PHẦN TRẮC NGHIỆM ( 5,0 điểm)

Câu 1: Tập nghiệm của bất phương trình \(\dfrac{{2x - 3}}{3} > \dfrac{{x - 1}}{2}\) là

A. \(\left( {3; + \infty } \right)\)

B. \(\left( { - 3; + \infty } \right)\)

C. \(\left( {2; + \infty } \right)\)     

D. \(\left( { - 2; + \infty } \right)\)

Câu 2: Biểu thức \(f\left( x \right) = 3x + 5\) nhận giá trị dương khi và chỉ khi:

A. \(x \ge  - \dfrac{5}{3}.\)   B. \(x >  - \dfrac{5}{3}.\)

C. \(x <  - \dfrac{5}{3}.\)     D. \(x > \dfrac{5}{3}.\)

Câu 3: Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + 2y - 3 < 0\\2x + y - 2 > 0\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất  phương trình đã cho?

A. \(M\left( {2;3} \right)\).     

B. \(N\left( {2;2} \right)\).

C. \(P\left( {3; - 1} \right)\).   

D. \(Q\left( { - 1; - 5} \right)\).

Câu 4: Cho biểu thức \(f\left( x \right) = a{x^2} + bx + c(a \ne 0)\) và \(\Delta  = {b^2} - 4ac\). Chọn khẳng định đúng?

A. Khi \(\Delta  > 0\) thì \(f\left( x \right)\) luôn  trái dấu hệ số a với mọi \(x \in \mathbb{R}\).

B. Khi \(\Delta  = 0\) thì \(f\left( x \right)\) trái dấu với hệ số a với mọi \(x \ne  - \dfrac{b}{{2a}}\)

C. Khi \(\Delta  < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số a với mọi \(x \ne  - \dfrac{b}{{2a}}\).

D. Khi \(\Delta  < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số a với mọi \(x \in \mathbb{R}\).

Câu 5: Tìm tập nghiệm của bất phương trình \( - {x^2} + 2016x + 2017 > 0\).       

A. \(\left( { - 1;2017} \right).\)                  

B. \(\left( { - \infty ; - 1} \right) \cup \left( {2017; + \infty } \right).\)        

C. \(\left( { - \infty ; - 1} \right] \cup \left[ {2017; + \infty } \right).\)     

D. \(\left[ { - 1;2017} \right].\)

Câu 6: Tìm tất cả các giá trị của tham số \(m\) đề bất phương trình \({x^2} + \left( {2m + 1} \right)x + {m^2} + 2m - 1 > 0\) nghiệm đúng với mọi \(x\)

A. \(m < \dfrac{5}{4}\).                B. \(m > \dfrac{5}{4}\)

C. \(m <  - \dfrac{5}{4}\).              D. \(m >  - \dfrac{5}{4}\).

Câu 7: Kết quả điểm kiểm tra môn Toán của 40 học sinh lớp 10A được trình bày ở bảng sau

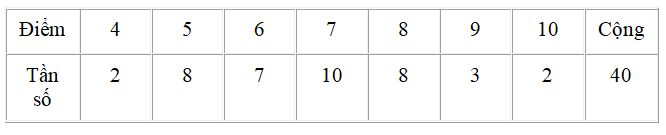
Tính số trung bình cộng của bảng trên.( làm tròn kết quả đến một chữ số thập phân).

 A. \(7,0\).                    B. \(6,4\).

C. \(6,8\).                     D. \(6,7\).

Câu 8: Cho \(0 < \alpha  < \dfrac{\pi }{2}\).  Hãy chọn khẳng định đúng? 

A. \(\tan \alpha  < 0\).              B. \(\sin \alpha  < 0\).

C. \(\cos \alpha  < 0\).              D.\(\sin \alpha  > 0\)

Câu 9: Chọn khẳng định đúng ?

A. \(1 + {\tan ^2}x = \dfrac{1}{{{{\cos }^2}x}}\)   .

B. \({\sin ^2}x - {\cos ^2}x = 1\)    .   

C. \(\tan x =  - \dfrac{1}{{\cot x}}\)    .

D. \(\sin x + \cos x = 1\).

Câu 10: Chọn khẳng định đúng?

A. \(\cot \left( {\pi  - \alpha } \right) = \cot \alpha \).

B. \(\cos \left( {\pi  - \alpha } \right) =  - \cos \alpha \).

C. \(\tan \left( {\pi  - \alpha } \right) = \tan \alpha \).

D. \(\sin \left( {\pi  - \alpha } \right) =  - \sin \alpha \).

Câu 11: Tính giá trị của biểu thức \(P = \dfrac{{2\sin \alpha  - 3\cos \alpha }}{{4\sin \alpha  + 5\cos \alpha }}\) biết \(\cot \alpha  =  - 3\)

A. \(\dfrac{9}{7}\).                             B. \(\dfrac{7}{9}\).

C. \( - 1\).                             D. \(1\).

Câu 12: Với mọi \(a,b\).  Khẳng định nào dưới đây đúng?

A. \(sin(a + b) = sina.sinb + cosa.cosb\).      

B. \(cos(a + b) = cosa.\sin b - sina.\cos b\).

C. \(cos(a + b) = cosa.cosb + sina.sinb\).

D. \(sin(a + b) = sina.cosb + sinb.cosa\).

Câu 13: Với mọi \(a\).  Khẳng định nào dưới đây sai?

A. \(\sin acosa = 2\sin 2a\).

B. \(2co{s^2}a = cos2a + 1\).

C. \(2si{n^2}a = 1 - cos2a\).

D. \(co{s^2}a - si{n^2}a = cos2a\).

Câu 14: Tìm một vectơ chỉ phương của đường thẳng \(d:\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 3 - 5t\end{array} \right.\)

 A\(\overrightarrow u  = (5;2)\).                   B. \(\overrightarrow u  = (2; - 5)\).

C. \(\overrightarrow u  = ( - 1;3)\).              D. \(\overrightarrow u  = ( - 3;1)\).

Câu 15. Trong mặt phẳng \(Oxy\) cho hai điểm \(A\left( {1; - 3} \right),B\left( { - 2;5} \right)\). Viết phương trình tổng quát đi qua hai điểm \(A,B\)

A. \( - 3x + 8y - 30 = 0\).

B. \(8x + 3y - 1 = 0\) .      

C. \(8x + 3y + 1 = 0\).

D. \( - 3x + 8y + 30 = 0\).

Câu 16: Trong mặt phẳng \(Oxy\) cho hai điểm \(M(2;5)\) và \(N(5;1)\). Phương trình đường thẳng đi qua \(M\) và cách \(N\) một đoạn có độ dài bằng \(3\)là

A. \(y + 2 = 0\) hoặc \(24x + 7y + 134 = 0\)

B. \(y - 2 = 0\) hoặc \(24x + 7y - 134 = 0\)

C. \(x + 2 = 0\) hoặc \(7x + 24y + 134 = 0\)

D. \(x - 2 = 0\) hoặc \(7x + 24y - 134 = 0\)

Câu 17: Trong mặt phẳng \(Oxy\) cho \(\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Tọa độ tâm \(I\)và bán kính\(R\)của đường tròn \(\left( C \right)\)là

A. \(I\left( {3; - 2} \right),R = 3\).

B. \(I\left( {2; - 3} \right),R = 3\) .

C. \(I\left( { - 2;3} \right),R = 3\) .

D. \(I\left( { - 3;2} \right),R = 3\).

Câu 18: Bán kính của đường tròn tâm \(I( - 2; - 1)\)và tiếp xúc với đường thẳng \(4x - 3y + 10 = 0\) là                                

A. \(R = \dfrac{1}{5}\)                       B. \(R = 1\)

C. R=\(3\)                    D. \(R = \sqrt 5 \)

Câu 19. Trong mặt phẳng \(Oxy\) cho \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 4\).  Viết phương trình tiếp tuyến của đường tròn \(\left( C \right)\), biết tiếp tuyến song song với \(d:4x - 3y + 5 = 0\).

A. \(3x + 4y - 1 = 0\) hoặc \(3x + 4y - 21 = 0\).     

B. \(4x - 3y + 1 = 0\) hoặc \(4x - 3y + 21 = 0\).      

C. \(4x - 3y - 1 = 0\) hoặc \(4x - 3y - 21 = 0\).

D. \(3x + 4y + 1 = 0\) hoặc \(3x + 4y + 21 = 0\).

Câu 20. Trong mặt phẳng \(Oxy\) cho \(\left( E \right):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{9} = 1\). Tọa độ hai tiêu điểm của Elip là

A. \({F_1}\left( { - 8;0} \right),{F_2}\left( {8;0} \right)\).

B. \({F_1}\left( {0; - 4} \right),{F_2}\left( {0;4} \right)\).           

C. \({F_1}\left( {0; - 8} \right),{F_2}\left( {0;8} \right)\).

D. \({F_1}\left( { - 4;0} \right),{F_2}\left( {4;0} \right)\).

II. PHẦN TỰ LUẬN (5,0 điểm)

Bài 1: ( 1,5 điểm) Giải bất phương trình sau: \(\dfrac{{\left( { - x + 3} \right)\left( {{x^2} + 3x - 4} \right)}}{{ - {x^2} + 4x - 4}} > 0\)

Bài 2: ( 2,0 điểm)

a. Chứng minh rằng: \(\dfrac{{{{(\sin x + \cos x)}^2} - 1}}{{\cot x - \sin x\cos x}} = 2{\tan ^2}x\)

b. Cho \(\cos \alpha  =  - \dfrac{1}{4}\) và \(\dfrac{\pi }{2}\langle \alpha \langle \pi \). Tính \(\sin 2\alpha ,\cos 2\alpha \)

Bài 3: (1,0 điểm) Trong mặt phẳng \({\rm{Ox}}y\), cho tam giác ABC biết \(A(3;7)\,\,\)và \(\,\,B(1;1),C( - 5;1)\). Tìm tọa độ trung điểm \(M\) của đoạn thẳng \(BC\). Viết phương trình đường trung tuyến \(AM\).

Bài 4: (0,5 điểm) Trong mặt phẳng \({\rm{Ox}}y\), cho \(M( - 1;1),N(1; - 3)\). Viết phương trình đường tròn đi qua hai điểm \(M,N\) và có tâm  nằm trên đường thẳng \(d:2x - y + 1 = 0\).

Lời giải chi tiết

I. Trắc nghiệm

1	2	3	4	5
A	B	C	D	A
6	7	8	9	10
B	C	D	A	B
11	12	13	14	15
C	D	A	B	C
16	17	18	19	20
D	A	B	C	D

 II. Tự luận

Bài 1: Giải bất phương trình sau: \(\dfrac{{\left( { - x + 3} \right)\left( {{x^2} + 3x - 4} \right)}}{{ - {x^2} + 4x - 4}} > 0\)

\(\begin{array}{l} - x + 3 = 0 \Leftrightarrow x = 3\\\,{x^2} + 3x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 4\\x = 1\end{array} \right.\\ - {x^2} + 4x - 4 = 0 \Leftrightarrow x = 2\end{array}\)

Bảng xét dấu:

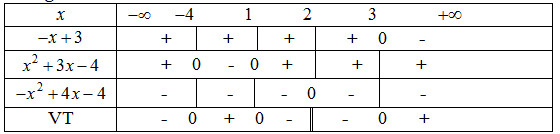
Vậy tập nghiệm của bpt là:  \(S = \left( { - 4;1} \right) \cup \left( {3; + \infty } \right)\).

Bài 2:

a. Chứng minh rằng: \(\dfrac{{{{(\sin x + \cos x)}^2} - 1}}{{\cot x - \sin x\cos x}} = 2{\tan ^2}x\)

\(VT = \dfrac{{{{\sin }^2}x + {{\cos }^2}x + 2\sin x\cos x - 1}}{{\cos x\left( {\dfrac{1}{{\sin x}} - \sin x} \right)}}\)  

     \( = \dfrac{{2\sin x\cos x}}{{\cos x\left( {\dfrac{{1 - {{\sin }^2}x}}{{\sin x}}} \right)}}\)

   \( = \dfrac{{2{{\sin }^2}x}}{{{{\cos }^2}x}} = 2{\tan ^2}x = VP\)

b. Cho \(\cos \alpha  =  - \dfrac{1}{4};\,\,\,\dfrac{\pi }{2} < \alpha  < \pi \). Tính \(\sin 2\alpha ,\cos 2\alpha \).

Ta có: \({\sin ^2}\alpha  = 1 - {\cos ^2}\alpha  = 1 - \dfrac{1}{{16}} = \dfrac{{15}}{{16}}\)

\(\Rightarrow \sin \alpha  =  \pm \sqrt {\dfrac{{15}}{{16}}}  =  \pm \dfrac{{\sqrt {15} }}{4}\)

Vì \(\dfrac{\pi }{2}<\alpha < \pi \) nên \(\sin \alpha >0\) nên \(\sin \alpha  = \dfrac{{\sqrt {15} }}{4}\).

Ta có:   \(\sin 2x = 2\sin x\cos x \)\(\,= 2\dfrac{{\sqrt {15} }}{4}.\left( { - \dfrac{1}{4}} \right) =  - \dfrac{{\sqrt {15} }}{8}\)

Ta có: \(\cos 2x = 2{\cos ^2}x - 1 \)\(\,= 2{\left( { - \dfrac{1}{4}} \right)^2} - 1 =  - \dfrac{7}{8}\)

Bài 3: Gọi I là trung điểm của đoạn thẳng BC, ta có:

\(\left\{ \begin{array}{l}{x_I} = \dfrac{{1 + ( - 5)}}{2} =  - 2\\{y_I} = \dfrac{{1 + 1}}{2} = 1\end{array} \right. \Rightarrow M( - 2;1)\)

Ta có  \(\overrightarrow {AM}  = ( - 5; - 6)\)là một vectơ chỉ phương của đường thẳng BM

Suy ra một vectơ pháp tuyến của AM là \(\overrightarrow n  = (6; - 5)\)

Đường thẳng  AM qua \(A(3;7)\)và có vectơ pháp tuyến \(\overrightarrow n  = (6; - 5)\) có phương trình tổng quát là: \(6(x - 3) - 5(y - 7) = 0 \) \(\Leftrightarrow 6x - 5y + 17 = 0\)

Bài 4:

Ta có  \(\left\{ \begin{array}{l}I(a;b) \in d\\IA = IB\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2a - b + 1 = 0\\{\left( { - 1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {1 - a} \right)^2} + {\left( { - 3 - b} \right)^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2a - b + 1 = 0\\a - 2b - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{4}{3}\\b =  - \dfrac{5}{3}\end{array} \right.\)  \(\) 

Và bán kính \(R = IA = \dfrac{{\sqrt {65} }}{3}\)

Vậy phương trình đường tròn cần tìm là \({\left( {x + \dfrac{4}{3}} \right)^2} + {\left( {y + \dfrac{5}{3}} \right)^2} = \dfrac{{65}}{9}\)