Đề số 6 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10

Đề bài

I. PHẦN TRẮC NGHIỆM (20 câu; 4,0 điểm).

Câu 1: Tìm giá trị của tham số \(m\)để phương trình \({x^2} - 3mx - m - 5 = 0\) có nghiệm \(x =  - 2\).

A. \(m =  - \dfrac{1}{5}\). 

B. \(m = \dfrac{1}{5}\).

C. \(m = 5\).                      

D. \(m =  - 5\).

Câu 2: Tìm tập nghiệm \(S\)của bất phương trình \((x - 2)(x + 3) \ge 0\).

A. \(S = ( - \infty ; - 3) \cup (2; + \infty )\).

B. \(S = ( - 3;2)\).           

C. \(S = \left[ { - 3;2} \right]\).

D. \(S = \left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\).

Câu 3: Cho tam giác \(ABC\) có \(a = 5cm,{\rm{ }}c = 9cm,{\rm{ }}\cos C =  - \dfrac{1}{{10}}\). Tính độ dài đường cao \({h_a}\) hạ từ \(A\)của tam giác \(ABC\).

A. \({h_a} = \dfrac{{\sqrt {462} }}{{40}}cm\).

B. \({h_a} = \dfrac{{\sqrt {462} }}{{10}}cm\). 

C. \({h_a} = \dfrac{{21\sqrt {11} }}{{40}}cm\).

D. \({h_a} = \dfrac{{21\sqrt {11} }}{{10}}cm\).

Câu 4: Cho \(\sin x =  - \dfrac{4}{5}\) với \(\pi  < x < \dfrac{{3\pi }}{2}\). Tính giá trị của biểu thức \(P = \cos x + \sin x\).

A. \(P =  - \dfrac{{11}}{{25}}\).                         

B. \(P =  - \dfrac{9}{{25}}\).

C. \(P =  - \dfrac{1}{5}\).                                       

D. \(P =  - \dfrac{7}{5}\).

Câu 5: Tìm tập nghiệm \(T\)của bất phương trình \(\sqrt { - {x^2} + 3x + 4}  \le x - 2\).

A. \(T = \left[ {\dfrac{7}{2};4} \right]\).

B. \(T = \left( { - \infty ;2} \right] \cup \left[ {4; + \infty } \right)\).

C. \(T = \left( { - \infty ;\dfrac{7}{2}} \right] \cup \left[ {4; + \infty } \right)\).

D. \(T = \left[ {2;\dfrac{7}{2}} \right]\).

Câu 6: Tìm tập hợp các giá trị của tham số \(m\)để phương trình \({x^2} - 2(m - 2)x - m + 14 = 0\) vô nghiệm.

A. \(\left( { - 2;5} \right)\).

B. \(( - \infty ; - 2) \cup (5; + \infty )\).           

C. \(( - 2;7)\).

D. \(\left( { - \infty ; - 2} \right] \cup \left[ {7; + \infty } \right)\).

Câu 7: Tìm tập các giá trị của tham số \(m\)để phương trình \(2x - \sqrt {x - 3}  - m = 0\) có nghiệm.

A. \(m \ge 6\).

B. \(\dfrac{{47}}{8} \le m < 6\).

C. \(m \ge \dfrac{{47}}{8}\).

D. \(\dfrac{{47}}{8} < m \le 6\).

Câu 8: Tìm tập hợp các giá trị của \(x\)để bất phương trình \((x - 3)\sqrt {{x^2} + 4}  \le {x^2} - 9\) vô nghiệm.

A. \(\left( {3; + \infty } \right)\)

B. \(\left( { - \infty  - \dfrac{5}{6}} \right] \cup \left[ {3; + \infty } \right)\).

C. \(\left( { - \infty ; - \dfrac{5}{6}} \right)\)

D. \(\left( { - \dfrac{5}{6};3} \right)\).

Câu 9: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho 2 đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 2 + t\\y =  - 3t\end{array} \right.(t \in \mathbb{R})\), \({\rm{ }}{d_2}:2x + y - 5 = 0\). Tìm tọa độ giao điểm \(M\) của \({d_1}\) và \({d_2}\).

A. \(M( - 1; - 3)\).            B. \(M(3;1)\).

C. \(M(1;3)\).                    D. \(M(3; - 3)\).

Câu 10: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(d:\left\{ \begin{array}{l}x =  - 2 + 3t\\y = 1 - 5t\end{array} \right.(t \in \mathbb{R})\). Vectơ nào dưới đây là vectơ chỉ phương của \(d\)?

A. \(\overrightarrow u  = ( - 2;1)\).                  

B. \(\overrightarrow u  = (3; - 5)\).

C. \(\overrightarrow u  = (1;2)\).                      

D. \(\overrightarrow u  = (5;3)\).

Câu 11: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \((C)\): \({x^2} + {y^2} - 2x - 2y - 2 = 0\) và đường thẳng\({\rm{ }}d:3x - 4y - 4 = 0\). Tìm phương trình đường thẳng \(\Delta \) song song với\({\rm{ }}d\) cắt \((C)\) tại 2 điểm \(A,{\rm{ }}B\) sao cho độ dài đoạn \(AB = 2\sqrt 3 \).

A. \({\rm{ }}\Delta :3x - 4y - 4 = 0\).

B. \({\rm{ }}\Delta :4x - 3y + 6 = 0\).              

C. \({\rm{ }}\Delta :3x - 4y + 6 = 0\).

D. \({\rm{ }}\Delta :4x - 3y - 6 = 0\).

Câu 12: Cho tam giác \(ABC\) có \(BC = a,{\rm{ }}AC = b,{\rm{ }}AB = c\). Tìm khẳng định SAI.

A. \({c^2} = {a^2} + {b^2} - 2ab\cos C\).

B. \({b^2} = {a^2} + {c^2} - 2ac\cos B\).     

C. \({a^2} = {b^2} + {c^2} - 2bc\cos B\).

D. \({a^2} = {b^2} + {c^2} - 2bc\cos A\).

Câu 13: Tìm điều kiện xác định bất phương trình \(\sqrt {3 - x}  + \dfrac{1}{{\sqrt {x + 2} }} - 2 > 0\).

A. \(x \in ( - \infty ; - 2) \cup \left[ {3; + \infty } \right)\).

B. \(x \in \left( { - 2;3} \right]\).                          

C. \(x \in \left[ { - 2;3} \right)\).

D. \(x \in \left( { - \infty ; - 2} \right] \cup \left( {3; + \infty } \right)\).

Câu 14: Tìm tất cả các giá trị của tham số \(m\)để phương trình \({x^2} - 2(m + 1)x + m - 2 = 0\) có 2 nghiệm trái dấu.

A. \(m > 2\).                       B. \(m <  - 1\).

C. \(m < 2\).                       D. \(m >  - 1\).

Câu 15: Với điều kiện xác định. Tìm đẳng thức nào đúng ?

A. \(1 + {\cot ^2}x = \dfrac{1}{{{{\cos }^2}x}}\).

B. \({\sin ^2}x + {\cos ^2}x = 1\).                      

C. \(\tan x + \cot x = 1\).

D. \(1 + ta{n^2}x =  - \dfrac{1}{{{{\sin }^2}x}}\).

Câu 16: Tìm tập nghiệm \(S\)của bất phương trình \( - {x^2} + 4x + 5 > 0\).

A. \(S = ( - \infty ; - 1) \cup (5; + \infty )\).

B. \(S = ( - \infty ; - 5) \cup (1; + \infty )\).

C. \(S = ( - 1;5)\).

D. \(S = ( - 5;1)\).

Câu 17: Tìm tập nghiệm \(S\)của bất phương trình \(\dfrac{{{x^2} - 4x + 3}}{{x + 1}} \le 0\).

A. \(S = \left( { - \infty ; - 1} \right] \cup \left[ {1;3} \right]\).

B. \(S = \left( { - 1;1} \right] \cup \left[ {3; + \infty } \right)\).       

C. \(S = ( - 1;1) \cup \left[ {3; + \infty } \right)\).

D. \(S = ( - \infty ; - 1) \cup \left[ {1;3} \right]\).

Câu 18: Cho tam thức \(f(x) = (1 - m){x^2} - 2(m - 1)x + m \)\(\,- 3\). Tìm tập hợp các giá trị của tham số \(m\)để bất phương trình \(f(x) \ge 0\) vô nghiệm.

A. \(\left[ {1;2} \right)\).                               B. \(\left( {2; + \infty } \right)\).

C. \(\left( { - \infty ;1} \right)\).                           D. \(\left( {1;2} \right)\).

Câu 19: Trong mặt phẳng với hệ tọa độ \(Oxy\), cho 2 điểm \(A( - 1;1)\), \(B(5; - 3)\). Viết phương trình đường tròn đường kính \(AB\).

A. \({(x - 2)^2} + {(y + 1)^2} = 13\).

B. \({(x + 2)^2} + {(y - 1)^2} = 5\).

C. \({(x + 2)^2} + {(y - 1)^2} = 13\).

D. \({(x - 2)^2} + {(y + 1)^2} = 5\).

Câu 20: Cho tam giác \(ABC\) có \(\widehat B = {120^o}\), cạnh \(AC = 2\sqrt 3 cm\). Tìm bán kính \(R\)của đường tròn ngoại tiếp tam giác \(ABC\).

A. \(R = 3cm\).                 B. \(R = 1cm\).

C. \(R = 4cm\).                 D. \(R = 2cm\).

II. PHẦN TỰ LUẬN (6,0 điểm)

Câu 1 (1,5 điểm). Giải các bất phương trình sau:

a). \(({x^2} - 7x + 12)(5 - x) > 0\).

b). \(\dfrac{{2{{(x - 1)}^2} + 1}}{{{x^2} - x - 6}} + \dfrac{1}{2} \le 0\). 

Câu 2 (1,5 điểm). Cho phương trình \({x^2} - 2(m - 3)x + 5 - m = 0\) (*) với \(m\)là tham số.

a). Giải phương trình  (*) khi \(m = 1\).

b). Tìm tất cả các giá trị của tham số \(m\)để phương trình (*) có 2 nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\) thỏa \({x_1} < {x_2} < 1\).

Câu 3 (1,0 điểm). Cho \(\cos x =  - \dfrac{8}{9}\) và \(\dfrac{\pi }{2} < x < \pi \). Tính giá trị của \(\sin x,{\rm{ }}\cot x.\)

Câu 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có đỉnh \(A(1;2)\) và phương trình đường trung tuyến \(BM:2x + y + 1 = 0\), \(M \in AC\).

a). Viết phương trình đường thẳng \(d\)qua \(A\)và vuông góc với đường thẳng \(BM\).

b). Viết phương trình đường tròn \((C)\) có tâm \(A\)và tiếp xúc với đường thẳng \(BM\).

c). Tìm tọa độ điểm \(B\), biết \(CD:x + y - 1 = 0\) là phương trình đường phân giác trong của góc \(C\).

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM (20 câu; 4,0 điểm).

1	2	3	4	5
B	D	D	D	A
6	7	8	9	10
A	C	D	C	B
11	12	13	14	15
C	C	B	C	B
16	17	18	19	20
C	D	A	A	D

II. PHẦN TỰ LUẬN (6,0 điểm)

Câu 1 (1,5 điểm). Giải các bất phương trình sau:

a). \(({x^2} - 7x + 12)(5 - x) > 0\)

Ta có \({x^2} - 7x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 4\end{array} \right.;\)  \(5 - x = 0 \Leftrightarrow x = 5\)

Bảng xét dấu:

 Vậy BPT có nghiệm: \(x \in \left( { - \infty ;3} \right) \cup \left( {4;5} \right)\)

b). \(\dfrac{{2{{(x - 1)}^2} + 1}}{{{x^2} - x - 6}} + \dfrac{1}{2} \le 0 \)

\(\Leftrightarrow \dfrac{{5{x^2} - 9x}}{{2{x^2} - 2x - 12}} \le 0\).    

Ta có \(5{x^2} - 9x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{9}{5}\end{array} \right.;\)    \(2{x^2} - 2x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 2\end{array} \right.\)

Bảng xét dấu :

Vậy BPT có nghiệm: \(x \in \left( { - 2;0} \right] \cup \left[ {\dfrac{9}{5};3} \right)\)

Câu 2 (1,5 điểm). Cho phương trình \({x^2} - 2(m - 3)x + 5 - m = 0\) (*) với \(m\)là tham số.

a) Giải phương trình  (*) khi \(m = 1\).

Khi \(m = 1\), ta có PT : \({x^2} + 4x + 4 = 0 \Leftrightarrow x =  - 2\)

b) Tìm tất cả các giá trị của tham số \(m\)để phương trình (*) có 2 nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\) thỏa \({x_1} < {x_2} < 1\).

Ta có \({\Delta '} = {m^2} - 5m + 4\)

Để PT có 2 nghiệm phân biệt \( \Leftrightarrow {\Delta '} > 0 \)

\(\Leftrightarrow {m^2} - 5m + 4 > 0 \)

\(\Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 4\end{array} \right.\,\,\,\,\,\,\left( 1 \right);\)

Do \({x_1} < {x_2} < 1 \) \(\Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} - 2 < 0\\{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) + 1 > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2(m - 3) - 2 < 0\\5 - m - 2(m - 3) + 1 > 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2m - 8 < 0\\ - 3m + 12 > 0\end{array} \right. \Leftrightarrow m < 4\,\,\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(m < 1\) thì PT có 2 nghiệm phân biệt \({x_1},{\rm{ }}{x_2}\) thỏa \({x_1} < {x_2} < 1\).

Câu 3 (1,0 điểm). Cho \(\cos x =  - \dfrac{8}{9}\) và \(\dfrac{\pi }{2} < x < \pi \). Tính giá trị của \(\sin x,{\rm{ }}\cot x.\)

Ta có \({\sin ^2}x + {\cos ^2}x = 1\) \( \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x = \dfrac{{17}}{{81}}\); Do \(\dfrac{\pi }{2} < x < \pi  \) \(\Rightarrow \sin \,x = \dfrac{{\sqrt {17} }}{9}\)

Mặt khác \(\cot x = \dfrac{{\cos x}}{{\sin \,x}} =  - \dfrac{{8\sqrt {17} }}{{17}}\)

Câu 4 (2,0 điểm). Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có đỉnh \(A(1;2)\) và phương trình đường trung tuyến \(BM:2x + y + 1 = 0\), \(M \in AC\).

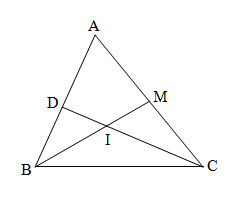
a). Viết phương trình đường thẳng \(d\)qua \(A\)và vuông góc với đường thẳng \(BM\).

Ta có: - Đường thẳng \(d\)qua \(A(1;2)\)

Do \(d \bot BM \Rightarrow \) \(d\) có VTCP \(\overrightarrow a  = \left( {2;1} \right)\)

\( \Rightarrow d\) có PTTS: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\end{array} \right.\)

b). Viết phương trình đường tròn \((C)\) có tâm \(A\)và tiếp xúc với đường thẳng \(BM\).

Ta có: Đường tròn \((C)\) có tâm \(A(1;2)\)

Do \((C)\) tiếp xúc với \(BM\)\( \Rightarrow R = d\left( {A;BM} \right) = \dfrac{{\left| {2.1 + 2 + 1} \right|}}{{\sqrt 5 }} \)\(\,= \sqrt 5 \)

\( \Rightarrow (C)\) có PT: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 5\)

c). Tìm tọa độ điểm \(B\), biết \(CD:x + y - 1 = 0\) là phương trình đường phân giác trong của góc \(C\).

- Gọi \(M\left( {a; - 2a - 1} \right) \in BM\)

- \(M\) là trung điểm của \(AC \Rightarrow C\left( {2a - 1; - 4a - 4} \right)\)

- \(C \in CD \Rightarrow \left( {2a - 1} \right) + \left( { - 4a - 4} \right) - 1 \)\(\,= 0\) \( \Rightarrow a =  - 3\)

\( \Rightarrow \left\{ \begin{array}{l}M\left( { - 3;5} \right)\\C\left( { - 7;8} \right)\end{array} \right.\)

- \(B\left( {b; - 2b - 1} \right) \in BM,\,\,\left( {B \ne M} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}\cos \left( {CM;CD} \right) = \dfrac{7}{{5\sqrt 2 }}\\\cos \left( {CB;CD} \right) = \dfrac{{\left| {3b + 16} \right|}}{{\sqrt 2 \sqrt {5{b^2} + 50b + 130} }}\end{array} \right.\)

- Theo đề bài, ta có: \(\cos \left( {CM;CD} \right) = \cos \left( {CB;CD} \right)\)

\(\begin{array}{l} \Leftrightarrow \dfrac{7}{{5\sqrt 2 }} = \dfrac{{\left| {3b + 16} \right|}}{{\sqrt 2 \sqrt {5{b^2} + 50b + 130} }}\\ \Leftrightarrow 20{b^2} + 50b - 30 = 0\\ \Leftrightarrow \left[ \begin{array}{l}b =  - 3\,\,\left( l \right)\\b = \dfrac{1}{2}\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

\( \Rightarrow B\left( {\dfrac{1}{2}; - 2} \right)\)