Đề kiểm tra 15 phút - Đề số 5 - Bài 7 - Chương 3 - Hình học 9

Đề bài

Từ điểm M ở ngoài đường tròn (O), kẻ cát tuyến MAB ( A nằm giữa hai điểm M và B) và các tiếp tuyến MC, MD. Gọi H là giao điểm của OM và CD.

a)   Chứng minh : MC² = MA.MB.

b)  Chứng minh tứ giác AHOB nội tiếp.

Lời giải chi tiết

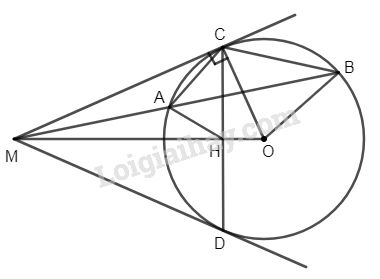
a) Xét \(∆MAC\) và \(∆MCB\) có:

+) \(\widehat M\) chung,

+) \(\widehat {MCA} = \widehat {MBC}\) ( góc giữa tiếp tuyến một dây và góc nội tiếp cùng chắn cung AC)

Do đó \(∆MAC\) đồng dạng \(∆MCB\) (g.g)

\( \Rightarrow\dfrac {{MA} }{ {MC}} =\dfrac {{MC}}{{MB}} \)

\(\Rightarrow MA.MB = M{C^2}\;\;\;\;(1)\) 

b)   Dễ thấy MO là đường trung trực của đoạn CD ( vì \(OC = OD = R, MC = MD\)) nên \(MO \bot CD\) tại H.

Trong tam giác vuông MCO có CH là đường cao.

Ta có : \(MO.MH = MC^2 \;\;\;    (2)\)  ( hệ thức lượng trong tam giác vuông )

Từ (1) và (2) \( \Rightarrow  MA.MB = MO.MH\).

Do đó \(∆MAH\) đồng dạng \(∆MOB\) (g.g) \(\Rightarrow \widehat {MHA} = \widehat {MBO}\) chứng tỏ tứ giác AHOB nội tiếp.