Bài 59 trang 90 SGK Toán 9 tập 2
Giải bài 59 trang 90 SGK Toán 9 tập 2. Cho hình bình hành ABCD
Đề bài
Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)
Phương pháp giải - Xem chi tiết
+) Số đo tổng hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\)
+) Sử dụng tính chất hai đường thẳng song song, tính chất hình bình hành.
Lời giải chi tiết
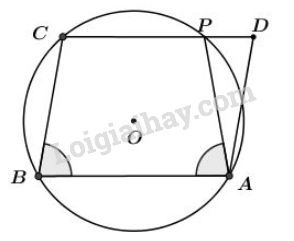
Do tứ giác \(ABCP\) nội tiếp nên ta có:
\(\widehat{BAP} + \widehat{BCP} = 180^0.\) (1)
Ta lại có: \(\widehat{ABC}+ \widehat{BCP}= 180^0\) (hai góc trong cùng phía do \(CD//AB\)). (2)
Từ (1) và (2) suy ra: \(\widehat{BAP}= \widehat{ABC}.\)
Vậy \(ABCP\) là hình thang cân, suy ra \(AP = BC.\) (3)
Mà \(BC = AD\) (hai cạnh đối của hình bình hành) (4)
Từ (3) và (4) suy ra \(AP = AD\) (đpcm).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 59 trang 90 SGK Toán 9 tập 2 timdapan.com"







