Đề kiểm tra 15 phút - Đề số 15 - Bài 4, 5 - Chương 1 - Hình học 8

Đề bài

Dựng hình thang cân ABCD \(\left( {AB// CD} \right)\) biết AB = a, đường chéo AC = m, góc giữa hai đường chéo là \(\alpha .\)

Lời giải chi tiết

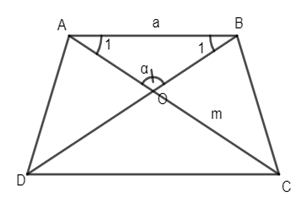
Giả sử hình thang cân ABCD đã dựng ta thấy tam giác cân AOB dựng được ngay biết \(AB = a,\widehat {AOB} = \alpha \)

\( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}} = \dfrac{{{{180}^ \circ } - \alpha } }{2} = {90^ \circ } -\dfrac{\alpha  }{2}\)

Cần xác định hai đỉnh C và D.

+D thuộc BO sao cho BD = m.

+C thuộc tia AO sao cho AC = m.

Từ đó dựng \(\Delta AOB\) biết AB = a, \(\widehat {OAB} = \widehat {OBA} = {90^ \circ } - \dfrac{\alpha }{2}.\)

- Lấy D thuộc tia BO sao cho BD = m.

- Lấy C thuộc tia AO sao cho AC = m.

Ta được hình thang ABCD cần dựng.

Khi \(0 < \alpha  < {180^ \circ }\) bài toán luôn có nghiệm hình.