Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8
Giải Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8
Đề bài
Cho tam giác ABC có ba góc nhọn, các đường cao BH, CK. Gọi D, E lần lượt là hình chiếu của B và C lên đường thẳng HK. Gọi M là trung điểm của BC.
a) Chứng minh \(\Delta MKH\) cân.
b) Chứng minh DK = HE.
Lời giải chi tiết
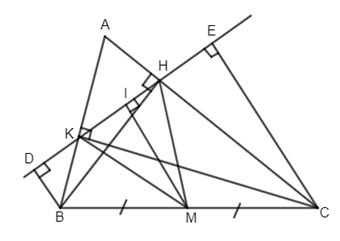
a) Ta có MH, MK là các trung tuyến của các tam giác vuông BHC và BKC có chung cạnh huyền BC nên MH = MK.
Vậy \(\Delta MKH\) cân.
b) Kẻ \(MI \bot DE,\) ta có MI là đường trung bình của hình thang vuông BDEC
\( \Rightarrow I\) là trung điểm của DE hay \(ID = IE\;\;(1)\)
Mặt khác \(\Delta MKH\) cân có đường cao MI đồng thơi là trung tuyến nên IK = IH (2)
Từ (1) và (2) \( \Rightarrow ID - IK = IE - IH\) hay \(DK = HE.\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 12 - Bài 4, 5 - Chương 1 - Hình học 8 timdapan.com"







