Bài 48 trang 12 SBT Hình Học 11 Nâng cao

Đề bài

Cho hình thanh ABCD vuông tại A và D, hình thang A'B'C'D' vuông góc tại A' và D'. 

Chứng minh rằng hai hình thang ấy bằng nhau nếu AB = A’B’, BC = B^’C^’ và CD = C^’D’.

Lời giải chi tiết

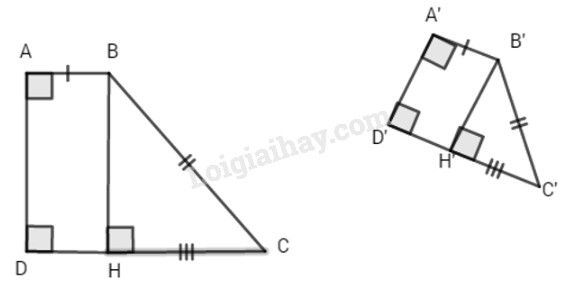
Nếu AB = CD thì kết quả là hiển nhiên.

Giả sử AB < CD, kẻ BH\(\bot\) CD, B'H' \(\bot\) C'D'

Ta có CH = CD – AB = C'D' - A'B' = C'H'.

Từ đó, suy ra hai tam giác vuông BHC và B'H'C' bằng nhau.

Gọi F là phép dời hình biến tam giác BHC thành tam giác B'H'C', thì dễ thấy rằng F biến A thành A' và biến D thành D'.

Do đó F biến hình thang ABCD thành hình thang A'B'C'D'.

Vậy hai hình thang đó bằng nhau.