Bài 45 trang 12 SBT Hình Học 11 nâng cao
Giải bài 45 trang 12 sách bài tập Hình Học 11 nâng cao. Chứng minh rằng tâm của bốn hình vuông đó làm thành một tứ giác có hai đường chéo bằng nhau và vuông góc với nhau.
Đề bài
Về phía ngoài của tứ giác lồi ABCD dựng các hình vuông có cạnh lần lượt là AB, BC, CD, DA. Chứng minh rằng tâm của bốn hình vuông đó làm thành một tứ giác có hai đường chéo bằng nhau và vuông góc với nhau.
Lời giải chi tiết
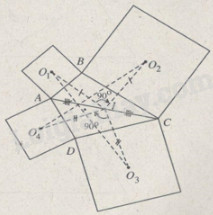
Gọi \({O_1},\,{O_2},\,{O_3},\,{O_4}\) là tâm hình vuông có cạnh lần lượt là AB, BC, CD, DA và I là trung điểm của đoạn thẳng AC.
Xét tam giác ABC và tam giác ACD thì theo kết quả bài tập 43 ta có \(I{O_1}{O_2}\) và \(I{O_4}{O_3}\) là những tam giác vuông cân.
Từ đó, Suy ra phép quay tâm I góc quay \( - {90^o}\) biến \({O_1}\) thành \({O_2}\) và biến \({O_3}\) thành \({O_4}\).
Do đó, ta có:
\({O_1}{O_3} = {O_2}{O_4}\) và \({O_1}{O_3} \bot {O_2}{O_4}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 45 trang 12 SBT Hình Học 11 nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 45 trang 12 SBT Hình Học 11 nâng cao timdapan.com"







