Bài 4 trang 99 SGK Hình học 10

Cho tam giác \(ABC\) đều có cạnh bằng \(6cm\). Một điểm \(M\) nằm trên cạnh \(BC\) sao cho \(BM  = 2cm\)

LG a

Tính độ dài của đoạn thẳng \(AM\) và tính cosin của góc \(BAM\)

Lời giải chi tiết:

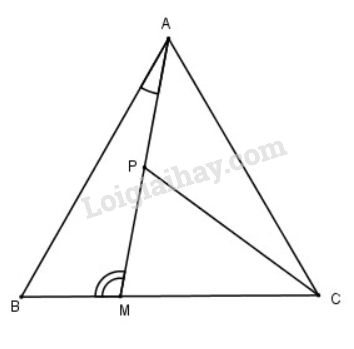
Theo định lí cosin trong tam giác ABM ta có:

\( A{M^2} = B{A^2} + B{M^2}\)\( - 2BA.BM.\cos\widehat {ABM}\)

\(\eqalign{
& \Rightarrow A{M^2} = 36 + 4 - 2.6.2.{1 \over 2} \cr 
& \Rightarrow A{M^2} = 28 \Rightarrow AM = 2\sqrt 7 (cm) \cr} \)

Ta cũng có:

\(\eqalign{
& \cos \widehat {BAM }= {{A{B^2} + A{M^2} - B{M^2}} \over {2AB.AM}} \cr 
& \Rightarrow \cos\widehat { BAM }= {{5\sqrt 7 } \over {14}} \cr} \)

LG b

Tính bán kính đường tròn ngoại tiếp tam giác \(ABM.\)

Lời giải chi tiết:

Trong tam giác \(ABM\), theo định lí Sin ta có:

\(\eqalign{
& {{AM} \over {\sin \widehat {ABM}}} = 2R \Leftrightarrow R = {{AM} \over {2\sin \widehat {ABM}}} \cr 
& R = {{2\sqrt 7 } \over {2\sin {{60}^0}}} = {{2\sqrt {21} } \over 3}(cm) \cr} \)

LG c

Tính độ dài đường trung tuyến vẽ từ \(C\) của tam giác \(ACM.\)

Lời giải chi tiết:

Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.

Áp dụng công thức đường trung tuyến trong tam giác CAM ta có:

\(\eqalign{
& C{P^2} = {{C{A^2} + C{M^2}} \over 2} - {{A{M^2}} \over 4} \cr 
& \Rightarrow C{P^2} = {{36 + 16} \over 2} - {{28} \over 4} \cr 
& \Rightarrow C{P^2} = 19 \Rightarrow CP = \sqrt {19} \cr}\)

LG d

Tính diện tích tam giác \(ABM.\)

Lời giải chi tiết:

Diện tích tam giác \(\displaystyle ABM\) là:

\(\displaystyle S = {1 \over 2}BA.BM\sin \widehat {ABM} \)\(\displaystyle = {1 \over 2}6.2\sin {60^0} = 3\sqrt 3 (c{m^2})\)