Câu 35 trang 120 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho tam giác ABC vuông tại B. Lấy điểm D bất kì trên đường thẳng vuông góc với mặt phẳng (ABC) kẻ từ điểm A \((S ≢ A)\). Gọi B₁, C₁ lần lượt là hình chiếu của điểm A trên SB và SC. Chứng minh rằng khi điểm S thay đổi thì

a) Giao tuyến của mặt phẳng (ABC) và mặt phẳng (AB₁C₁) là đường thẳng cố định và là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.

b) Đường thẳng B₁C₁ đi qua điểm cố định I và \(\widehat {IAB} = \widehat {IC{\rm{A}}}\).

Lời giải chi tiết

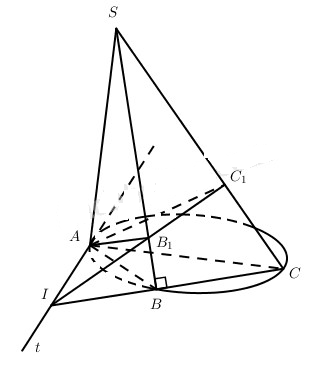
a) Dễ chứng minh được \(SC \bot \left( {A{B_1}{C_1}} \right)\). Gọi At là giao tuyến của (ABC) và (AB₁C₁) thì \(At \bot SC\). Mặt khác \(SA \bot \left( {ABC} \right)\) nên \(At \bot AC\). Vậy đường thẳng At là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.

b) Kí hiệu I là giao điểm của At và đường thẳng BC thì I là điểm có định, mặt khác các điểm I, B₁, C₁ thuộc cả hai mặt phẳng (AB₁C₁) và (SBC), do đó các điểm I, B₁, C₁ thẳng hàng, tức là đường thẳng B₁C₁ đi qua điểm cố định I khi S thay đổi trên đường thẳng kẻ từ A vuông góc với mp(ABC).

Cũng từ chứng minh trên ta có \(\widehat {IAB} = \widehat {IC{\rm{A}}}\) (cùng chắn cung AB của đường tròn ngoại tiếp tam giác ABC).