Câu 23 trang 118 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho tứ diện ABCD có \(C{\rm{D}} = {4 \over 3}AB\). Gọi I, J, K lần lượt là trung điểm của BC, AC, BD. Cho biết \(JK = {5 \over 6}AB\), tính góc giữa đường thẳng CD với các đường thẳng IJ và AB.

Lời giải chi tiết

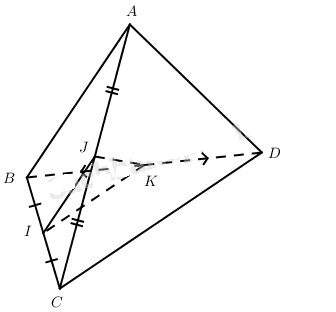
Ta có:

\(\eqalign{  & IJ = {1 \over 2}AB  \cr  & IK = {1 \over 2}CD = {2 \over 3}AB  \cr  & I{J^2} + I{K^2} = {1 \over 4}A{B^2} + {4 \over 9}A{B^2}  \cr  &  = {{25} \over {36}}A{B^2} \cr} \)

mà \(I{K^2} = {{25} \over {36}}A{B^2}\)  nên \(I{J^2} + I{K^2} = J{K^2}\)

Vậy \(JI \bot IK\) .

Do IJ // AB, IK // CD nên góc giữa AB và CD bằng 90°

Mặt khác IJ // AB mà  AB ⊥ CD nên IJ ⊥ CD

Vậy góc giữa IJ và CD bằng 90°.