Câu 29 trang 119 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 29 trang 119 Sách bài tập Hình học 11 Nâng cao
Đề bài
Cho hình chóp S.ABC có SB vuông góc với mp(ABC), ABC là tam giác vuông tại A.
a) Chứng minh rằng ACS là tam giác vuông.
b) Tính SA, SB, SC biết rằng \(\widehat {ACB} = \alpha ,\widehat {ACS} = \beta \) và BC = a.
Lời giải chi tiết
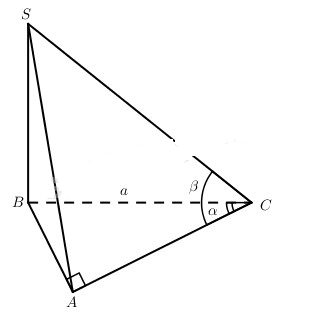
a) \(SA \bot \left( {ABC} \right)\) và \(BA \bot AC\) nên \(SA \bot AC\) tức là SAC là tam giác vuông tại A.
b) Ta có
\(\eqalign{ & AC = a\cos \alpha \cr & SA = AC\tan \beta = a\cos \alpha \tan \beta \cr & SC = {{AC} \over {\cos \beta }} = {{a\cos \alpha } \over {\cos \beta }} \cr & S{B^2} = S{C^2} - B{C^2} \cr & = {{{a^2}{{\cos }^2}\alpha } \over {{{\cos }^2}\beta }} - {a^2} \cr & = {{{a^2}\left( {{{\cos }^2}\alpha - {{\cos }^2}\beta } \right)} \over {{{\cos }^2}\beta }} \cr & \Rightarrow SB = {a \over {\cos \beta }}.\sqrt {{{\cos }^2}\alpha - {{\cos }^2}\beta } \cr} \)
(Điều kiện để Câu toán có nghĩa là α, β phải thỏa mãn \({\cos ^2}\alpha > {\cos ^2}\beta \)).
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 29 trang 119 Sách bài tập Hình học 11 Nâng cao timdapan.com"







