Bài tập 6 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính diện tích xung quanh, diện tích toàn phần của các hình chóp đều với kích thước đã cho trên hình sau đây:
Đề bài
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp đều với kích thước đã cho trên hình sau đây:
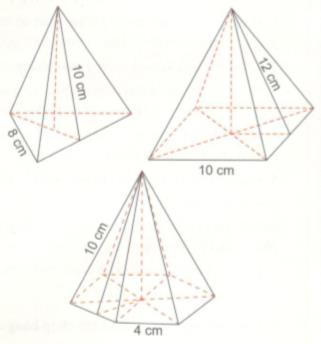
Lời giải chi tiết
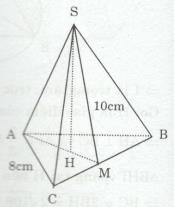
• Diện tích xung quanh của hình chóp đều
\(\eqalign{ & {S_{xq}} = p.d \cr&\;\;\;= {1 \over 2}(AB + BC + AC).SM \cr &\;\;\; = {1 \over 2}(8 + 8 + 8).10 = 120(c{m^2}) \cr} \)
Ta có \(CM = {{BC} \over 2} = {8 \over 2} = 4(cm)\)
∆ABC đều có AM là đường trung tuyến
=> AM cũng là đường cao \( \Rightarrow AM \bot BC\) tại M
Chiều cao của tam giác đáy là: \(AM = \sqrt {A{C^2} - M{C^2}} = \sqrt {{8^2} - {4^2}} \)\(\, = \sqrt {48} (cm)\)
Diện tích đáy của hình chóp đều: \({S_d} = {1 \over 2}AM.BC = {1 \over 2}\sqrt {48} .8 \)\(\,= 4\sqrt {48} (c{m^2})\)
Diện tích toàn phần của hình chóp đều là: \({S_{tp}} = {S_{xq}} + {S_d} = (120 + 4\sqrt {48} )(c{m^2})\)
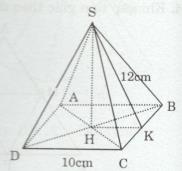
• Diện tích đáy của hình chóp đều:
\({S_d} = D{C^2} = {10^2} = 100(c{m^2})\)
Diện tích xung quanh của hình chóp đều:
\({S_{xq}} = p.d = (10 + 10).SK = 20.12 \)\(\,= 240(c{m^2})\)
Diện tích toàn phần của hình chóp đều:
\({S_{tp}} = {S_{xq}} + {S_d} = 240 + 100 \)\(\,= 340(c{m^2})\)
• Vì MNOPQR là lục giác đều nên các tam giác MHN, NHO, OHP, PHQ, QHR và RHM là sáu tam giác đều bằng nhau. Đường cao \(HK = \sqrt {H{M^2} - K{M^2}} \)
\( \Rightarrow HK = \sqrt {{4^2} - {2^2}} = \sqrt {12} (cm)\)
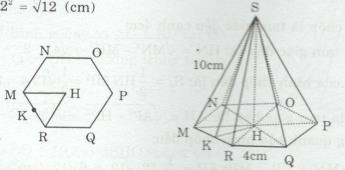
Diện tích đáy của hình chóp: \({S_d} = 6{S_{MHR}} = 6.{1 \over 2}HK.MR \)\(\,= 6{1 \over 2}\sqrt {12} .4 = 12\sqrt {12} (c{m^2})\)
Đường cao của mỗi mặt bên hay trung đoạn của hình chóp đều:
\(d = SK = \sqrt {S{M^2} - M{K^2}} \)\(\, = \sqrt {{{10}^2} - {2^2}} = \sqrt {96} (cm)\)
Diện tích xung quanh của hình chóp đều:
\({S_{xq}} = p.d = {1 \over 2}.6RQ.SK = 3.4.\sqrt {96} \)\(\,= 12\sqrt {96} (c{m^2})\)
Diện tích toàn phần của hình chóp đều: \({S_{tp}} = {S_{xq}} + {S_d} = (\sqrt {96} + 12\sqrt {96} ) \)\(\,= 13\sqrt {96} (c{m^2})\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 6 trang 122 Tài liệu dạy – học Toán 8 tập 2 timdapan.com"







