Bài tập 3 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính thể tích của một hình chóp tam giác đều, biết chiều cao của hình chóp là 8 cm, bán kính đường tròn ngoại tiếp tam giác đáy bằng 12 cm.
Đề bài
Tính thể tích của một hình chóp tam giác đều, biết chiều cao của hình chóp là 8 cm, bán kính đường tròn ngoại tiếp tam giác đáy bằng 12 cm.
Lời giải chi tiết
Gọi I là tâm đường tròn ngoại tiếp ∆ABC đều
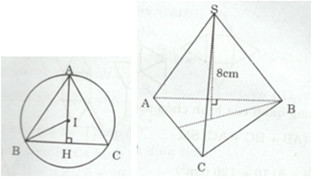
=> I là trọng tâm, trực tâm của ∆ABC
Gọi H là giao điểm của AI và BC
\( \Rightarrow AH \bot BC\) và \(AI = {2 \over 3}AH \)
\(\Rightarrow AH = {{3AI} \over 2} = {{3.12} \over 2} = 18(cm) \)
\(\Rightarrow IH = AH - AI = 6(cm)\)
∆BHI vuông tại H nên \(BH = \sqrt {B{I^2} - I{H^2}} = \sqrt {{{12}^2} - {6^2}} \)\(\,= \sqrt {108} (cm)\)
\( \Rightarrow BC = 2BH = 2\sqrt {108} (cm)\)
Thể tích của hình chóp tam giác đều:
\(\eqalign{ & V = {1 \over 3}{S_{ABC}}.h = {1 \over 3}.{1 \over 2}AH.BC.h \cr & = {1 \over 3}.{1 \over 2}.18.2\sqrt {108} .8 = 48\sqrt {108} (c{m^3}) \cr} \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập 3 trang 122 Tài liệu dạy – học Toán 8 tập 2 timdapan.com"







