Bài 9 trang 52 SGK Hình học 10 nâng cao
Cho tam giác ABC với ba đường trung tuyến AD, BE, CF. Chứng minh rằng
Đề bài
Cho tam giác \(ABC\) với ba đường trung tuyến \(AD, BE, CF\). Chứng minh rằng
\(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} = 0\).
Phương pháp giải - Xem chi tiết
Dựa vào quy tắc trung điểm - vecto, thay các vecto AD, BE, CF bởi tổng 2 vecto khác chung gốc.
Lời giải chi tiết
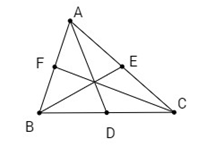
Vì D là trung điểm của BC nên \(\overrightarrow {AD} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {AC} )\)
Tương tự vì E, F là trung điểm của AC, AB nên:
\(\eqalign{
& \overrightarrow {BE} = {1 \over 2}(\overrightarrow {BA} + \overrightarrow {BC} ) \cr
& \overrightarrow {CF} = {1 \over 2}(\overrightarrow {CA} + \overrightarrow {CB} ) \cr} \)
Do đó \(\overrightarrow {BC} .\overrightarrow {AD} + \overrightarrow {CA} .\overrightarrow {BE} + \overrightarrow {AB} .\overrightarrow {CF} \)
\(\eqalign{
& = {1 \over 2}\overrightarrow {BC} (\overrightarrow {AB} + \overrightarrow {AC} ) + {1 \over 2}\overrightarrow {CA} (\overrightarrow {BA} + \overrightarrow {BC} ) \cr&+ {1 \over 2}\overrightarrow {AB} (\overrightarrow {CA} + \overrightarrow {CB} ) \cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BA} \cr&+ \overrightarrow {CA} \overrightarrow {BC} + \overrightarrow {AB} \overrightarrow {CA} + \overrightarrow {AB} \overrightarrow {CB} )\cr
& = {1 \over 2}(\overrightarrow {BC} \overrightarrow {AB} + \overrightarrow {AB} \overrightarrow {CB} ) \cr&+ {1 \over 2}(\overrightarrow {BC} \overrightarrow {AC} + \overrightarrow {CA} \overrightarrow {BC} ) \cr&+ {1 \over 2}(\overrightarrow {CA} \overrightarrow {BA} + \overrightarrow {AB} \overrightarrow {CA} )\cr} \)
\(\begin{array}{l}
= \frac{1}{2}\overrightarrow {AB} \left( {\overrightarrow {BC} + \overrightarrow {CB} } \right)\\
+ \frac{1}{2}\overrightarrow {BC} \left( {\overrightarrow {AC} + \overrightarrow {CA} } \right)\\
+ \frac{1}{2}\overrightarrow {CA} \left( {\overrightarrow {BA} + \overrightarrow {AB} } \right)\\
= \frac{1}{2}\overrightarrow {AB} .\overrightarrow {BB} + \frac{1}{2}\overrightarrow {BC} .\overrightarrow {AA} + \frac{1}{2}\overrightarrow {CA} .\overrightarrow {BB} \\
= 0 + 0 + 0\\
= 0
\end{array}\)
(điều phải chứng minh)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9 trang 52 SGK Hình học 10 nâng cao timdapan.com"







