Bài 11 trang 52 SGK Hình học 10 nâng cao
Cho hai đường thẳng a và b cắt nhau tại M. Trên a có hai điểm A và B, trên b có hai điểm C và D
Đề bài
Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(M\). Trên \(a\) có hai điểm \(A\) và \(B\), trên \(b\) có hai điểm \(C\) và \(D\) đều khác \(M\) sao cho \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {MD} \,\,\). Chứng minh rằng bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.
Lời giải chi tiết
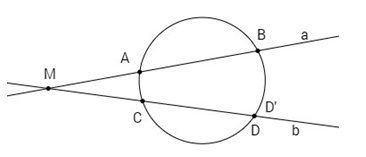
Gọi \((O)\) là đường tròn ngoại tiếp tam giác \(ABC\).
Gọi \(D'\) là giao điểm của \(b\) với \((O)\) ( \({D'} \ne C\)).
Theo giả thiết ta có \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {M{D}}\)
\(\eqalign{
& \Rightarrow \,\,\overrightarrow {MC} .\overrightarrow {MD} = \overrightarrow {MC} .\overrightarrow {M{D'}} \cr
& \Rightarrow \,\,\overrightarrow {MC} (\overrightarrow {MD} - \overrightarrow {M{D'}} ) = 0 \cr
& \Rightarrow \,\,\overrightarrow {MC} .\,\overrightarrow {{D'}D} = 0\,\,\,\, \cr} \)
\(\Rightarrow \,\overrightarrow {{D'}D} = 0\) (Do \(M, C, D, D'\) cùng thuộc đường thẳng b nên \(\overrightarrow {MC} \) và \(\overrightarrow {{D'}D}\) không thể vuông góc với nhau)
\( \Rightarrow D \equiv {D'}\).
Vậy bốn điểm \(A, B, C, D\) cùng nằm trên một đường tròn.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 11 trang 52 SGK Hình học 10 nâng cao timdapan.com"








