Bài 80 trang 155 SGK Đại số 10 nâng cao

Đề bài

Với giá trị nào của m, bất phương trình:

(m² + 1)x + m(x + 3) + 1 > 0 nghiệm đúng ∀x ∈ [-1; 2] ?

Lời giải chi tiết

Ta viết phương trình đã cho dưới dạng:

(m² + m + 1)x + 3m + 1 > 0

Đặt f(x) = (m² + m + 1)x + 3m + 1 ,

Với mỗi giá trị của m, đồ thị của hàm số y = f(x) là đường thẳng (D_m).

Gọi A_m và B_m là các điểm trên đường thẳng (Dm) có hoành độ theo thứ tự là – 1 và 2.

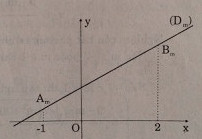
f(x) > 0 với ∀x ∈ [-1; 2] khi và chỉ khi đoạn thẳng A_mB_m nằm phía trên trục hoành. Điều này xảy ra khi và chỉ khi A_m và B_mnằm phía trên trục hoành, tức là: 

\(\left\{ \matrix{
f( - 1) > 0 \hfill \cr 
f(2) > 0 \hfill \cr} \right.\)

Thay f(-1) = -m² + 2m và f(2) = 2m²+ 5m + 3 , ta được hệ bất phương trình:

\(\left\{ \matrix{
- {m^2} + 2m > 0 \hfill \cr 
2{m^2} + 5m + 3 > 0 \hfill \cr} \right. \Leftrightarrow 0 < m < 2\)