Bài 75 trang 62 SGK giải tích 12 nâng cao

Cho hàm số: \(y = {x^4} - \left( {m + 1} \right){x^2} + m\)

LG a

Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.

Lời giải chi tiết:

Với \(m=2\) hàm số đã cho có dạng: \(y={x^4} - 3{x^2} + 2\)

Tập xác định: \(D=\mathbb R\)

\(\eqalign{
& y' = 4{x^3} - 6x \cr 
& y' = 0 \Leftrightarrow x\left( {4{x^2} - 6} \right) = 0\cr& \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = \frac{6}{4}\end{array} \right.\cr&\Leftrightarrow \left[ \matrix{x = 0 \hfill \cr x = {{\sqrt 6 } \over 2} \hfill \cr x = - {{\sqrt 6 } \over 2} \hfill \cr} \right. \cr} \)

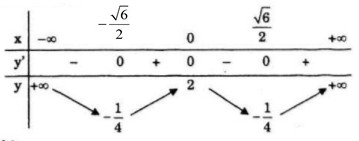
Hàm số đồng biến trên khoảng: \(\left( { - {{\sqrt 6 } \over 2};0} \right)\) và \(\left( {{{\sqrt 6 } \over 2}; + \infty } \right)\)

Hàm số nghịch biến trên khoảng: \(\left( { - \infty ; - {{\sqrt 6 } \over 2}} \right)\) và \(\left( {0;{{\sqrt 6 } \over 2}} \right)\)

Cực trị:

Hàm số đạt cực đại tại \(x=0;\,\,y(0)=2\)

Hàm số đạt cực tiểu tại \(x = {{\sqrt 6 } \over 2}\) và \(x =  - {{\sqrt 6 } \over 2}\), \(y\left( { \pm {{\sqrt 6 } \over 2}} \right) =  - {1 \over 4}\)

Giới hạn: \(\mathop {\lim }\limits_{x \to  \pm \infty } y =  + \infty \)

Bảng biến thiên:

Đồ thị:

Đồ thị cắt trục tung tại điểm \((0;2)\)

Đồ thị cắt trục hoành tại 4 điểm: \(\left( { - \sqrt 2 ;0} \right),\left( { - 1;0} \right),\) \(\left( {1;0} \right),\left( {\sqrt 2 ;0} \right)\)

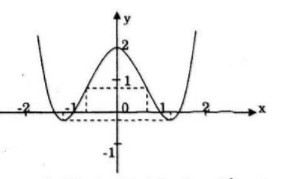
Đồ thị hàm số là hàm chẵn nhận trục Oy làm trục đối xứng.

LG b

Tìm các giá trị của m sao cho đồ thị của hàm số cắt trục hoành tại bốn điểm, tạo thành ba đoạn thẳng có độ dài bằng nhau.

Lời giải chi tiết:

Hoành độ giao điểm của đường cong (C) và trục là nghiệm phương trình 

\({x^4} - \left( {m + 1} \right){x^2} + m = 0\,\,\,\left( 1 \right)\)

\(\Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr 
{x^2} = m \hfill \cr} \right.\)

(1) có 4 nghiệm phân biệt khi và chỉ khi m>0 và \(m \ne 1\)

Khi đó (1) có 4 nghiệm: \(x =  - 1;\,x = 1;\,x =  - \sqrt m ;\,x = \sqrt m \)

* \( - \sqrt m  <  - 1 < 1 < \sqrt m \)

(C) cắt trục tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(\sqrt m  - 1 = 1 - \left( { - 1} \right) = 2 \Leftrightarrow m = 9\)

* \( - 1 <  - \sqrt m  < \sqrt m  < 1\)

(C) cắt trục hoành tại 4 điểm tạo thành ba đoạn thẳng bằng nhau khi \(1 - \sqrt m  = \sqrt m  - \left( { - \sqrt m } \right) = 2\sqrt m \)

Vậy m= 9 hoặc \(m = {1 \over 9}\).

Cách khác:

Đặt t=x², điều kiện t≥0.

Hoành độ giao điểm của đồ thị và trục hoành là nghiệm của phương trình:

x⁴-(m+1) x²+m=0 (1)

<=> t²-(m+1)t+m=0 (2)

Đồ thị của hàm số cắt trục tung tại bốn điểm tạo thành 3 đoạn thẳng có độ dai bằng nhau, tức 4 điểm có hoành độ lập thành cấp số cộng.

<=> Phương trình (2) có 2 nghiệm dương t₁,t₂ (với t₁ < t₂) thõa mãn điều kiện:

\(\begin{array}{l}\sqrt {{t_2}}  - \sqrt {{t_1}}  = \sqrt {{t_1}}  - \left( { - \sqrt {{t_1}} } \right)\\ \Leftrightarrow \sqrt {{t_2}}  = 3\sqrt {{t_1}} \\ \Leftrightarrow {t_2} = 9{t_1}\end{array}\)

Điều kiện để (2) có 2 nghiệm dương phân biệt là:

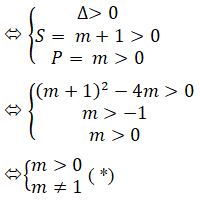
Kết hợp với điều kiện (*), vậy với m = 9 hoặc m = 1/9 thì đồ thị của hàm số cắt trục hoành tại 4 điểm, tạo thành 3 đoạn thẳng bằng nhau.