Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
Cho tứ diện ABCD có (widehat {CBD} = {90^0}.)
Đề bài
Cho tứ diện ABCD có \(\widehat {CBD} = {90^0}.\)
a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc
BC.
b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng
GK vuông góc với BC.
Phương pháp giải - Xem chi tiết
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
Lời giải chi tiết
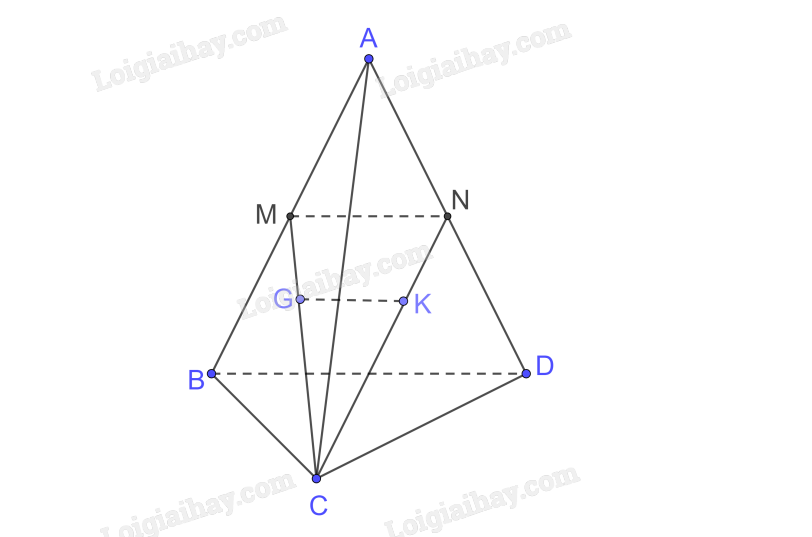
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức timdapan.com"







