Bài 7.26 trang 59 SGK Toán 11 tập 2 - Kết nối tri thức
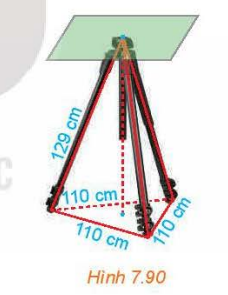
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm.
Đề bài
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 129 cm.
Phương pháp giải - Xem chi tiết
- Hình chóp đều là hình chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
- Một hình chóp là đều khi và chỉ khi đáy của nó là một hình đa giác đều và hình chiếu của đỉnh trên mặt phẳng đáy là tâm của mặt đáy.
Lời giải chi tiết
Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm nên hình chiếu của đỉnh là tâm của đáy mà đáy là tam giác đều do đó tâm là trọng tâm.
Vì đáy là tam giác đều cạnh 110 cm nên chiều cao của đáy bằng \(110.\frac{{\sqrt 3 }}{2} = 55\sqrt 3 \left( {cm} \right)\)
Khoảng cách từ gốc chân đến tâm là \(\frac{2}{3}.55\sqrt 3 = \frac{{110\sqrt 3 }}{3}\left( {cm} \right)\)
Chiều cao giá đỡ là \(\sqrt {{{129}^2} - {{\left( {\frac{{110\sqrt 3 }}{3}} \right)}^2}} = \sqrt {\frac{{37823}}{3}} \approx 112,28\left( {cm} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7.26 trang 59 SGK Toán 11 tập 2 - Kết nối tri thức timdapan.com"







