Bài 6 trang 109 SGK Toán 7 tập 1

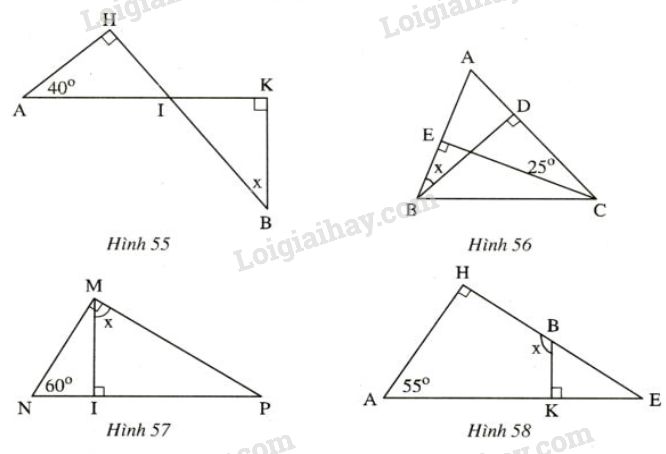
Đề bài

Tìm các số đo \(x\) ở các hình sau:

Lời giải chi tiết

Hình 55)

Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta áp dụng vào \(\Delta AHI\,\text{ có }\,\widehat H = {90^0}\) ta được: 

\(\widehat{A}+\widehat{AIH}= 90^0\),  (1)

Áp dụng vào \(\Delta BKI\,\text{ có }\,\widehat K = {90^0}\) ta được: 

\(\widehat{B} + \widehat{BIK} = 90^0\)   (2)

Mà  \(\widehat{AIH}= \widehat{BIK}\) (hai góc đối đỉnh)   (3)

Từ (1), (2) và (3) suy ra \(\widehat{A} = \widehat{B}\)

Vậy \(\widehat{B}=x= 40^0\)

Hình 56)

Áp dụng lí tổng hai góc nhọn của tam giác vuông phụ nhau ta áp dụng vào \(\Delta ABD\,\text{ có }\,\widehat {ADB} = {90^0}\) ta được:

 \(\widehat{ABD} +\widehat{A}= 90^0\),  (4)

Áp dụng vào \(\Delta ACE\,\text{ có }\,\widehat {AEC} = {90^0}\) ta được:

\(\widehat{ACE}+ \widehat{A}=90^0\),  (5)

Từ (4) và (5) suy ra \(\widehat{ACE} = \widehat{ABD}=25^0\)

Vậy \(x=25^0\)

Hình 57)

Ta có: \(\widehat{NMP}=\widehat{NMI} + \widehat{PMI}=  90^0\),  (6)

Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta áp dụng vào \(\Delta MNI\,\text{ có }\,\widehat {MIN} = {90^0}\) ta có :

\(\widehat{N } +  \widehat{NMI}=  90^0\),   (7)

Từ (6) và (7) suy ra \(\widehat{N } = \widehat{PMI}=60^0\)

Vậy \(x=60^0\)

Hình 58)

Theo định lí tổng hai góc nhọn của tam giác vuông phụ nhau ta  áp dụng vào \(\Delta AHE\,\text{ có }\,\widehat {AHE} = {90^0}\) ta có :

\(\widehat{E } + \widehat{A}=90^0\)

\(\widehat{E }= 90^0- \widehat{A} = 90^0- 55^0= 35^0\)

\(\widehat{KBH }=\widehat{BKE}+ \widehat{E }\) (góc ngoài tại đỉnh \(B\) của tam giác \(BKE\))

            \(= 90^0+ 35^0= 125^0\)

Vậy \(x=125^0\)