Bài 5 trang 108 SGK Toán 7 tập 1
Giải bài 5 trang 108 SGK Toán 7 tập 1. Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông trên hình 54.
Đề bài
Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông trên hình 54.
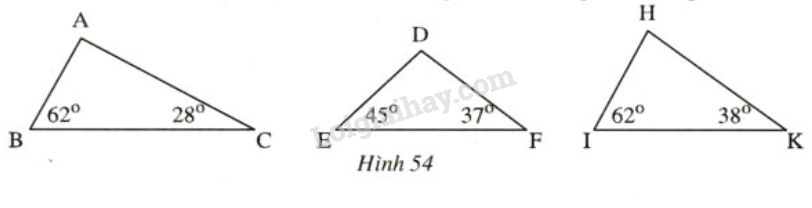
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí: Tổng ba góc của một tam giác bằng \({180^0}\)
+ Sử dụng định nghĩa tam giác nhọn, tam giác tù, tam giác vuông để gọi tên các tam giác.
Lời giải chi tiết
a) Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(ABC\) ta được:
$$\eqalign{
& \widehat A + \widehat B + \widehat C = {180^0} \cr
& \Rightarrow \widehat A = {180^0} - \widehat B - \widehat C \cr&\;\;\;\;\;\;\;\;\,= {180^0} - {62^0} - {28^0} = {90^0} \cr} $$
Do đó tam giác \(ABC\) vuông tại \(A\).
b) Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(DEF\) ta được:
$$\eqalign{
& \widehat D + \widehat E + \widehat F = {180^0} \cr
& \Rightarrow \widehat D = {180^0} - \widehat E - \widehat F \cr&\;\;\;\;\;\;\;\;\;\,= {180^0} - {45^0} - {37^0} = {98^0} \cr} $$
Do đó tam giác \(DEF\) tù.
c) Áp dụng định lí tổng ba góc của một tam giác vào tam giác \(HKI\) ta được:
$$\eqalign{
& \widehat H + \widehat K + \widehat I = {180^0} \cr
& \Rightarrow \widehat H = {180^0} - \widehat K - \widehat I \cr&\;\;\;\;\;\;\;\;\;\,= {180^0} - {38^0} - {62^0} = {80^0} \cr} $$
Do đó tam giác \(HKI\) nhọn.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5 trang 108 SGK Toán 7 tập 1 timdapan.com"







