Bài 45 trang 112 SGK Hình học 10 Nâng cao
Cho dây cung AB đi qua tiêu điểm của parabol (P). Chứng minh rằng khoảng cách từ trung điểm I của dây AB đến đường chuẩn của (P) bằng ({1 over 2}AB) . Từ đó có nhận xét gì về đường tròn đường kính AB?
Đề bài
Cho dây cung AB đi qua tiêu điểm của parabol (P). Chứng minh rằng khoảng cách từ trung điểm I của dây AB đến đường chuẩn của (P) bằng \({1 \over 2}AB\) . Từ đó có nhận xét gì về đường tròn đường kính AB?
Lời giải chi tiết
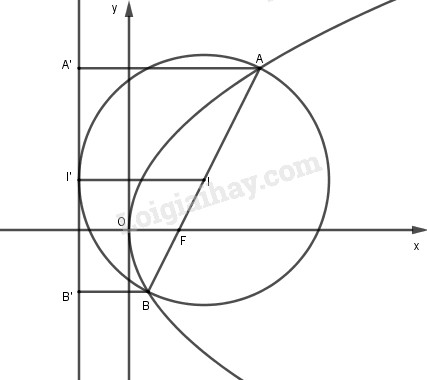
Gọi \(A',B',I'\) lần lượt là hình chiếu vuông góc của A,B,I lên đường chuẩn \(\Delta \)
Hình thang AA'B'B có I là trung điểm AB và II'//AA'//BB' nên II' là đường trung bình hình thang
\( \Rightarrow II' = \frac{{AA' + BB'}}{2} \) \(\Rightarrow AA' + BB' = 2II'\)
Theo định nghĩa parabol ta có:
\(AA' = AF\) và \(BB' = BF\)
\(\eqalign{
& \Rightarrow AB = AF+ FB \cr &= AA' + BB' = 2II' \cr
& \Rightarrow II' = d\left( {I,\Delta } \right) = {{AB} \over 2}. \cr} \)
Từ đó suy ra đường tròn đường kính AB tiếp xúc với đường chuẩn.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 45 trang 112 SGK Hình học 10 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 45 trang 112 SGK Hình học 10 Nâng cao timdapan.com"







