Bài 4 trang 31 SGK Hình học 12 Nâng cao

Cho khối lăng trụ đứng \(ABC.A’B'C’\) có diện tích đáy bằng \(S\) và \(AA' = h\). Một mặt phẳng \((P)\) cắt các cạnh \(AA', BB’, CC'\) lần lượt tại \({A_1},{B_1}\) và \(C_1\). Biết \(A{A_1} = a,B{B_1} = b,CC_1 = c\).

LG a

Tính thể tích hai phần của khối lăng trụ được phân chia bởi mặt phẳng \((P)\).

Lời giải chi tiết:

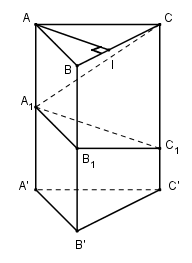
Kẻ đường cao \(AI\) của tam giác \(ABC\) thì \(AI \bot \left( {BCC'B'} \right)\)

\(\Rightarrow AI = d\left( {{A_1};\left( {BCC'B'} \right)} \right)\). Ta có:

\(\eqalign{
& {V_{_{ABC.{A_1}{B_1}{C_1}}}} = {V_{{A_1}.ABC}} + {V_{{A_1}BC{C_1}{B_1}}} \cr 
& = \frac{1}{3}A{A_1}.{S_{ABC}} + \frac{1}{3}{S_{BC{C_1}{B_1}}}.d\left( {{A_1},\left( {BC{C_1}{B_1}} \right)} \right)\cr &= {1 \over 3}{\rm{aS + }}{1 \over 3}{S_{BC{C_1}{B_1}}}.AI \cr 
& = {1 \over 3}aS + {1 \over 3}.{1 \over 2}\left( {b + c} \right).BC.AI \cr 
& = {1 \over 3}aS + {1 \over 3}\left( {b + c} \right)S \cr &= {1 \over 3}\left( {a + b + c} \right)S \cr 
& {V_{{A_1}{B_1}{C_1}A'B'C'}} = {V_{ABC.A'B'C'}} - {V_{ABC.{A_1}{B_1}{C_1}}} \cr 
& = Sh - {1 \over 3}\left( {a + b + c} \right)S \cr &= \frac{1}{3}S\left( {3h - a - b - c} \right) \cr} \)

Cách khác:

Không làm mất tính tổng quát, giả sử a≤b≤c.

Trên cạnh BB’ lấy B₂ sao cho BB₂=a

B₁B₂=b-a

Trên cạnh CC’ lấy C₂ sao cho CC₂=a

C₁C₂=c-a

Ta có: \({V_{ABC.{A_1}{B_1}{C_1}}} \) \(= {V_{ABC.{A_1}{B_2}{C_2}}} + {V_{{A_1}{B_2}{C_2}{B_1}}} + {V_{{A_1}{B_1}{C_2}{C_1}}}\)

Trong đó:

\(\begin{array}{l}{V_{ABC.{A_1}{B_2}{C_2}}} = A{A_1}.{S_{ABC}} = aS\left( 1 \right)\\{V_{{A_1}{B_2}{C_2}{B_1}}} = \frac{1}{3}{B_1}{B_2}.{S_{{A_1}{B_2}{C_2}}}\\ = \frac{1}{3}\left( {b - a} \right)S\left( 2 \right)\end{array}\)

(vì B₁ B₂⊥(A₁ B₂ C₂ ); ∆A₁ B₂ C₂=∆ABC)

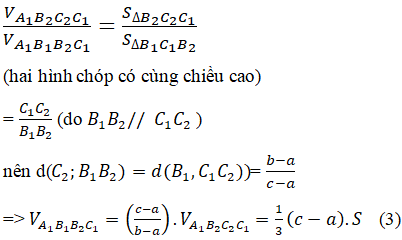
Thay (1), (2) và (3) vào (*) ta được:

LG b

Với điều kiện nào của \(a, b, c\) thì thể tích hai phần đó bằng nhau ?

Lời giải chi tiết:

\({V_{ABC.{A_1}{B_1}{C_1}}} = {V_{{A_1}{B_1}{C_1}.A'B'C'}} \) \(\Leftrightarrow {1 \over 3}\left( {a + b + c} \right)S = \frac{1}{3}S\left( {3h - a - b - c} \right) \) \( \Leftrightarrow a + b + c = 3h - a - b - c\) \(\Leftrightarrow 3h = 2\left( {a + b + c} \right)\)