Bài 1 trang 30 SGK Hình học 12 Nâng cao
Cho tứ diện ABCD có thể tích bằng V. Gọi B' và D' lần lượt là trung điểm của AB và AD. Mặt phắng (CB'D') chia khối tứ diện thành hai phần. Tính thể tích mỗi phần đó.
Đề bài
Cho tứ diện \(ABCD\) có thể tích bằng \(V\). Gọi \(B'\) và \(D'\) lần lượt là trung điểm của \(AB\) và \(AD\). Mặt phắng \((CB'D')\) chia khối tứ diện thành hai phần. Tính thể tích mỗi phần đó.
Lời giải chi tiết
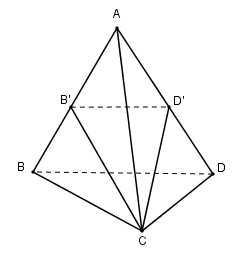
Mp \((CB’D’)\) chia khối tứ diện thành hai khối chóp \(C.AB’D’\) và \(C.BB’D’D\).
\(\frac{{{V_{AB'CD'}}}}{{{V_{ABCD}}}} = \frac{{AB'}}{{AB}}.\frac{{AC}}{{AC}}.\frac{{AD'}}{{AD}} \) \(= \frac{1}{2}.1.\frac{1}{2} = \frac{1}{4}\)
\(\Rightarrow {V_{A.B'CD'}} = \frac{1}{4}V \) \(\Rightarrow {V_{BCDB'D'}} = V - \frac{1}{4}V = \frac{3}{4}V\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 30 SGK Hình học 12 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1 trang 30 SGK Hình học 12 Nâng cao timdapan.com"