Bài 32 trang 96 Tài liệu dạy – học Toán 9 tập 2

Đề bài

Cho tam giác ABC nhọn và nội tiếp đường tròn O. Hai đường cao BE, CF của tam giác ABC cắt đường tròn O lần lượt tại K và I.

a) Chứng minh EF // IK.

b) IK cắt AB và AC lần lượt tại P và Q. Chứng minh \(OA \bot PQ\) .

c) Tia AO cắt (O) tại D, BE và CF cắt nhau tại H. Chứng minh tứ giác BHCD là hình bình hành.

d) Tia AH cắt (O) tại M. Chứng minh AB.DC = MB.AC.

e) Chứng minh BD.AC + CD.AB = AD.BC.

Lời giải chi tiết

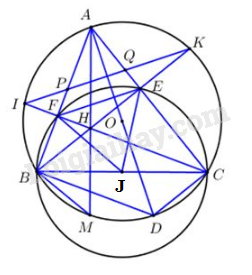
a) Gọi J là trung điểm của BC.

Tam giác BCE vuông tại E nên \(JE = \dfrac{1}{2}BC = JB = JC\) (định kí đường trung tuyến trong tam giác vuông).

Tam giác BCF vuông tại F nên \(JF = \dfrac{1}{2}BC = JB = JC\) (định kí đường trung tuyến trong tam giác vuông).

Từ đó suy ra \(JB = JC = JE = JF \Rightarrow \) 4 điểm B, C, E, F cùng thuộc đường tròn đường kính BC.

Xét đường tròn đường kính BC: \(\widehat {BEF} = \widehat {BCF} = \widehat {BCI}\) (hai góc nội tiếp cùng chắn cung BF).

Xét đường tròn \(\left( O \right)\): \(\widehat {BCI} = \widehat {BKI}\) (hai góc nội tiếp cùng chắn cung BI).

\( \Rightarrow \widehat {BEF} = \widehat {BKI}\). Mà hai góc này ở vị trí đồng vị bằng nhau \( \Rightarrow EF//KI\).

b) Xét đường tròn đường kính BC có \(\widehat {EBF} = \widehat {ECF}\) (hai góc nội tiếp cùng chắn cung EF) hay \(\widehat {ABK} = \widehat {ACI}\) .

Xét đường tròn \(\left( O \right)\) có  (hai góc nội tiếp bằng nhau chắn hai cung bằng nhau) \( \Rightarrow AI = AK\) (hai cung bằng nhau căng hai dây bằng nhau).

\( \Rightarrow A\) thuộc đường trung trực của IK.

Lại có \(OI = OK \Rightarrow \) O thuộc trung trực của IK.

\( \Rightarrow OA\) là trung trực của IK \( \Rightarrow OA \bot IK\) hay \(OI \bot PQ\) (do \(P,Q \in IK\))

c) Ta có \(\widehat {ABD} = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( O \right) \Rightarrow AB \bot BD\).

Mà \(CH \bot AB\,\,\left( {gt} \right) \Rightarrow CH//BD\).

\(\widehat {ACD} = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( O \right) \Rightarrow AC \bot CD\).

Mà \(BH \bot AC\,\,\left( {gt} \right) \Rightarrow BH//CD\)

Xét tứ giác BHCD có \(CH//BD;\,\,\,BH//CD \Rightarrow BHCD\) là hình bình hành (tứ giác có các cạnh cạnh đối song song).

d) Xét tứ giác \(AFHE\) có \(\widehat {AFH} + \widehat {AEH} = {90^0} + {90^0} = {180^0}\) nên \(AFHE\) là tứ giác nội tiếp

Suy ra \(\widehat {AFE} = \widehat {AHE}\) (hai góc nội tiếp cùng chắn cung AE trong đường tròn nội tiếp tứ giác \(AFHE\))

Mà \(\widehat {AHE} = \widehat {BHM}\) (hai góc đối đỉnh) nên \(\widehat {AFE} = \widehat {BHM}\)  (*)

Lại có tứ giác \(BFEC\) là tứ giác nội tiếp nên \(\widehat {AFE} = \widehat {BCA}\)  (**) (cùng bù với \(\widehat {BFE}\))

Xét đường tròn \(\left( O \right)\) có \(\widehat {BCA} = \widehat {BMA}\) (***)  (hai góc nội tiếp cùng chắn cung \(AB\))

Từ (*),  (**) và (***) ta có \(\widehat {BHM} = \widehat {BMH}\)

Suy ra tam giác \(BMH\) cân tại \(B\) nên \(BH = BM\)

Mà tứ giác \(BHCD\) là hình bình hành nên \(BH = CD\)

Suy ra \(BM = CD\)

Khi đó theo yêu cầu ta cần chứng minh \(AB.DC = MB.AC\)

Suy ra ta phải chứng minh \(AB = AC\), điều này mâu thuẫn với đề bài vì đề bài không hề cho tam giác ABC cân. Nên ta không thể có đẳng thức cần chứng minh.

e) 

Lấy điểm \(N\) trên \(AD\) sao cho \(\widehat {ACN} = \widehat {DCB}\).

Xét \(\Delta ACN\) và \(\Delta BCD\) có:
\(\widehat {ACN} = \widehat {BCD}\left( {gt} \right)\)
\(\widehat {DAC} = \widehat {DBC}\) (góc nội tiếp cùng chắn cung \(CD\))
\( \Rightarrow \Delta ACN \backsim \Delta BCD\left( {g - g} \right)\) \( \Rightarrow \dfrac{{AC}}{{BC}} = \dfrac{{AN}}{{BD}}\) (cạnh t/ư)
\( \Rightarrow AC.BD = BC.AN\) (1)
Ta có: \(\widehat {ACN} = \widehat {DCB}\)\( \Rightarrow \widehat {ACN} + \widehat {NCB} = \widehat {DCB} + \widehat {NCB}\) \( \Rightarrow \widehat {ACB} = \widehat {DCN}\)
Xét \(\Delta DCN\) và \(\Delta BCA\) có:
\(\widehat {CDN} = \widehat {ABC}\) (góc nội tiếp cùng chắn cung \(AC\))
\(\widehat {DCN} = \widehat {ACB}\left( {cmt} \right)\)
\( \Rightarrow \Delta DCN \backsim \Delta BCA\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{DC}}{{BC}} = \dfrac{{DN}}{{BA}}\) (cạnh t/ư)
\( \Rightarrow AB.CD = BC.DN\) (2)
Cộng (1) và (2) vế với vế ta được:
\(AC.BD + AB.CD = BC.AN + BC.DN\) \( = BC\left( {AN + DN} \right) = BC.AD\)
Vậy \(AC.BD + AB.CD = BC.AD\) (đpcm).