Bài 26 trang 67 SGK Toán 7 tập 2
Giải bài 26 trang 67 SGK Toán 7 tập 2. Chứng minh định lí:
Đề bài
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất tam giác cân và trung tuyến của tam giác, từ đó chứng minh hai tam giác bằng nhau.
Lời giải chi tiết
Giả sử \(∆ABC\) cân tại \(A\) có hai đường trung tuyến \(BM\) và \(CN\), ta chứng minh \(BM = CN.\)
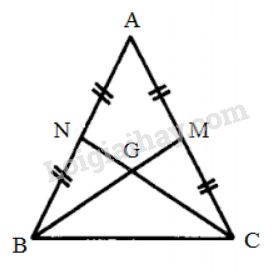
Vì \(∆ABC\) cân tại \(A\) nên \(AB = AC\)
Vì \(M, N\) lần lượt là trung điểm của \(2\) cạnh \(AC\) và \(AB\), suy ra:
\(AN = BN = AM = CM =\dfrac{AB}{2}\)\(\,= \dfrac{AC}{2}\).
Xét \(ΔBCM\) và \(ΔCBN\) có:
+) Cạnh \(BC\) chung
+) \(\widehat {BCM} = \widehat {CBN}\) (do \(ΔABC\) cân)
+) \(CM = BN\) (chứng minh trên)
Vậy \(ΔBCM = ΔCBN\) (c.g.c)
\(\Rightarrow BM = CN\) (điều phải chứng minh).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 67 SGK Toán 7 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 67 SGK Toán 7 tập 2 timdapan.com"







