Bài 19 trang 18 Sách giáo khoa (SGK) Hình học 10 Nâng cao

Đề bài

Chứng minh rằng \(\overrightarrow {AB}  = \overrightarrow {CD} \) khi và chỉ khi trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau.

Lời giải chi tiết

Giả sử \(\overrightarrow {AB}  = \overrightarrow {CD} \) và \(M, N\) lần lượt là trung điểm của \(AD,BC\).

Ta có \(\overrightarrow {MA}  + \overrightarrow {MD}  = \overrightarrow 0 \)

\(\overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0 \)\( \Rightarrow  - \overrightarrow {BN}  - \overrightarrow {CN}  = \overrightarrow 0  \)\(\Leftrightarrow  - \left( {\overrightarrow {BN}  + \overrightarrow {CN} } \right) = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {BN}  + \overrightarrow {CN}  = \overrightarrow 0 \)

và \(\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AB}  + \overrightarrow {BN}\)

\(\overrightarrow {MN}  = \overrightarrow {MD}  + \overrightarrow {DC}  + \overrightarrow {CN} \)

Suy ra

\(\eqalign{
& 2\overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {MN} \cr&= \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} + \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \cr 
&= \left( {\overrightarrow {MA} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BN} + \overrightarrow {CN} } \right) + \overrightarrow {AB} + \overrightarrow {DC} \cr 
&  = \overrightarrow 0  + \overrightarrow 0  + \overrightarrow {AB}  + \overrightarrow {DC} \cr&= \overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow {AB} - \overrightarrow {CD} \cr 
& = \overrightarrow 0 \cr} \)

Do đó, \(\overrightarrow {MN}  = \overrightarrow 0 \) , tức là \(M \equiv N\).

Vậy trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau.

Ngược lại, ta giả sử trung điểm của hai đoạn thẳng \(AD\) và \(BC\) trùng nhau, suy ra

\(\overrightarrow {MA}  + \overrightarrow {MD}  = \overrightarrow 0 ,\,\overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \)

Suy ra \(\overrightarrow {AB}  = \overrightarrow {AM}  + \overrightarrow {MB} \)\( = \overrightarrow {CM}  + \overrightarrow {MD}  = \overrightarrow {CD} \).

Cách khác:

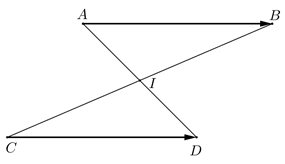
Ta chứng minh hai mệnh đề.

a) Cho \(\overrightarrow{AB}= \overrightarrow{CD}\) thì \(AD\) và \(BC\) có trung điểm trùng nhau.

Gọi \(I\) là trung điểm của \(AD\) ta chứng minh \(I\) cũng là trung điểm của \(BC\).

Theo quy tắc của ba điểm của tổng, ta có 

\(\overrightarrow{AB}= \overrightarrow{AI} + \overrightarrow{IB}\);

\(\overrightarrow{CD}= \overrightarrow{CI}+ \overrightarrow{ID}\)

Vì \(\overrightarrow{AB} = \overrightarrow{CD}\) nên \(\overrightarrow{AI} + \overrightarrow{IB}=  \overrightarrow{CI}+ \overrightarrow{ID}\)

\(\Rightarrow \overrightarrow{AI} - \overrightarrow{ID} = \overrightarrow{CI} - \overrightarrow{IB}\)

\(\Rightarrow\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{CI} + \overrightarrow{BI}\)    (1)

Vì \(I\) là trung điểm của \(AD\) nên \(\overrightarrow {IA}  + \overrightarrow {ID}  = \overrightarrow 0  \Leftrightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)  (2)

Từ (1) và (2) suy ra \(\overrightarrow{CI} + \overrightarrow{BI} = \overrightarrow{0} \Leftrightarrow \overrightarrow {IC}  + \overrightarrow {IB}  = \overrightarrow 0 \)  (3)

Đẳng thức (3) chứng tỏ \(I\) là trung điểm của \(BC\).

b) \(AD\) và \(BC\) có cùng trung điểm \(I\), ta chứng minh \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).

\(I\) là trung điểm của \(AD\) \( \Leftrightarrow \overrightarrow {IA}  + \overrightarrow {ID}  = \overrightarrow 0 \Rightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)   \(\Rightarrow\overrightarrow{AI} - \overrightarrow{ID} =\overrightarrow{0}\)

\(I\) là trung điểm của \(BC\) \( \Leftrightarrow \overrightarrow {IC}  + \overrightarrow {IB}  = \overrightarrow 0 \) \(\Rightarrow \overrightarrow{CI} + \overrightarrow{BI}= \overrightarrow{0}\)    \(\Rightarrow \overrightarrow{CI} - \overrightarrow{IB}= \overrightarrow{0}\)

Suy ra \(\overrightarrow{AI} - \overrightarrow{ID}=  \overrightarrow{CI}- \overrightarrow{IB}\) 

\(\Rightarrow \overrightarrow{AI} + \overrightarrow{IB} = \overrightarrow{CI}+ \overrightarrow{ID}\)    \(\Rightarrow \overrightarrow{AB}= \overrightarrow{CD}\) (đpcm)

Chú ý:

Các em có thể trình bày ngắn gọn như sau:

Gọi \(M,N\) là trung điểm của \(AD,BC\) ta có: \(\overrightarrow {AM}  = \overrightarrow {MD} ,\overrightarrow {BN}  = \overrightarrow {NC} \)

Do đó,

\(\begin{array}{l}\overrightarrow {AB}  = \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AM}  + \overrightarrow {MN}  + \overrightarrow {NB}  = \overrightarrow {CN}  + \overrightarrow {NM}  + \overrightarrow {MD} \\ \Leftrightarrow \left( {\overrightarrow {AM}  - \overrightarrow {MD} } \right) + \left( {\overrightarrow {MN}  - \overrightarrow {NM} } \right) + \left( {\overrightarrow {NB}  - \overrightarrow {CN} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow 0  + \left( {\overrightarrow {MM}  + \overrightarrow {MN} } \right) + \overrightarrow 0  = \overrightarrow 0 \\ \Leftrightarrow 2\overrightarrow {MN}  = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MN}  = \overrightarrow 0 \\ \Leftrightarrow M \equiv N\end{array}\)