Bài 19 trang 146 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Ở hình dưới, đường tròn (O) và (O’) tiếp xúc ngoài tại B
Đề bài
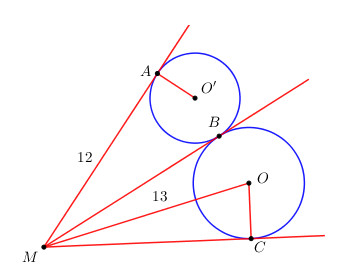
Ở hình dưới, đường tròn (O) và (O’) tiếp xúc ngoài tại B ; MB là tiếp tuyến chung trong của (O) và (O’), MA là tiếp tuyến của (O’), MC là tiếp tuyến của (O). Biết MA = 12, MO = 13. Tính bán kính của đường tròn (O).
Phương pháp giải - Xem chi tiết
Áp dụng tính chất 2 tiếp tuyến cắt nhau và định lí Pytago trong tam giác vuông.
Lời giải chi tiết
Xét đường tròn tâm \(\left( {O'} \right)\) có \(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau).
Xét đường tròn tâm \(\left( O \right)\) có \(MB = MC\) (tính chất 2 tiếp tuyến cắt nhau).
\( \Rightarrow MA = MB = MC = 12\).
Áp dụng định lí Pytago trong tam giác vuông \(OBC\) ta có :
\(OC = \sqrt {O{M^2} - M{C^2}} = \sqrt {{{13}^2} - {{12}^2}} \)\(\;= \sqrt {25} = 5\).
Vậy bán kính của đường tròn \(\left( O \right)\) bằng 5.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 19 trang 146 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







