Bài 18 trang 146 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A.
Đề bài
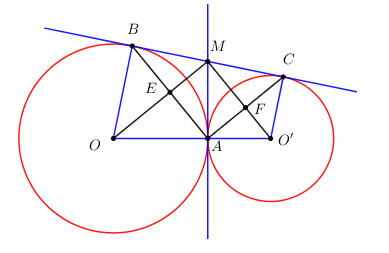
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. BC là tiếp tuyến chung ngoài, \(\left( {B \in \left( O \right),C \in \left( {O'} \right)} \right)\). Tiếp tuyến chung trong tại A cắt BC tại M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng :
a) Tứ giác AEMF là hình chữ nhật.
b) OO’ là tiếp tuyến của đường tròn đường kính BC.
Phương pháp giải - Xem chi tiết
a) Chứng minh tứ giác \(AEMF\) có \(\angle AEM = \angle AFM = \angle EMF = {90^0}\).
b) Chứng minh \(A\) thuộc đường tròn đường kính \(BC\), chứng minh \(MA \bot OO'\).
Lời giải chi tiết
a) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:
\(MO\) là tia phân giác của \(\angle AMB\) ;
\(MO'\) là tia phân giác của \(\angle AMC\).
Mà \(\angle AMB\) và \(\angle AMC\) là 2 góc kề bù \( \Rightarrow MO \bot MO'\) \( \Rightarrow \angle OMO' = {90^0}\) \( \Rightarrow \angle EMF = {90^0}\).
Ta có : \(OA = OB \Rightarrow O\) thuộc trung trực của \(AB\) ;
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB \Rightarrow OM \bot AB\)
\( \Rightarrow \angle AEM = {90^0}\).
Hoàn toàn tương tự ta chứng minh được \(O'M\) là trung trực của \(AC \Rightarrow O'M \bot AC\)
\( \Rightarrow \angle AFM = {90^0}\).
Xét tứ giác \(AEMF\) có : \(\angle AEM = \angle AFM = \angle EMF = {90^0} \) \(\Rightarrow \) \(AEMF\) là hình chữ nhật (Tứ giác có 3 góc vuông).
b) Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: \(\left\{ \begin{array}{l}MA = MB\\MA = MC\end{array} \right. \Rightarrow MB = MC \) \(\Rightarrow M\) là trung điểm của \(BC\).
\( \Rightarrow M\) là tâm đường tròn đường kính \(BC\).
Ta có : \(MA = MB = MC = \dfrac{1}{2}BC\) \( \Rightarrow \Delta ABC\) vuông tại \(A \Rightarrow \angle BAC = {90^0} \Rightarrow A\) thuộc đường tròn đường kính \(BC\) . Mà \(MA \bot OO'\,\,\left( {gt} \right) \Rightarrow OO'\) vuông góc với bán kính \(MA\) của đường tròn đường kính \(BC\) tại \(A\).
Vậy \(OO'\) là tiếp tuyến của đường tròn đường kính \(BC\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 146 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







