Bài 10 trang 146 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O ; R) đường kính AB. Vẽ dây AC sao cho AC = R.
Đề bài
Cho đường tròn (O ; R) đường kính AB. Vẽ dây AC sao cho AC = R.
a) Chứng minh rằng góc ACB bằng \({90^o}\), suy ra độ dài BC.
b) Gọi I là trung điểm của dây AC. OI cắt tiếp tuyến Ax của đường tròn (O) tại M. Chứng minh rằng OM là phân giác góc COA và MC là tiếp tuyến của đường tròn (O).
c) MC cắt tiếp tuyến By của đường tròn (O) tại N. Chứng minh rằng : MN = AM + BN và số đo góc MON bằng \({90^o}\).
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí đường trung tuyến trong tam giác vuông, áp dụng định lí Pytago.
b) Sử dụng quan hệ vuông góc giữa đường kính và dây cung và tính chất của tam giác cân. Chứng minh \(\angle OCM = {90^0}\).
c) Áp dụng tính chất 2 tiếp tuyến cắt nhau và mối quan hệ giữa tia phân giác của 2 góc kề bù.
Lời giải chi tiết
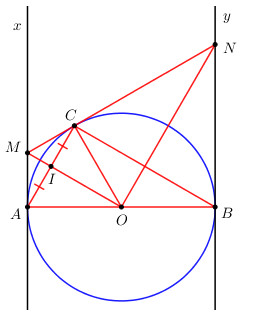
a) Ta có: \(OC = OA = OB = \dfrac{1}{2}AB \Rightarrow \Delta ABC\) vuông tại \(C\) (Định lí đường trung tuyến trong tam giác vuông)
\( \Rightarrow \angle ACB = {90^0}\).
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(B{C^2} = A{B^2} - A{C^2} = {\left( {2R} \right)^2} - {R^2} = 3{R^2}\)
\(\Leftrightarrow BC = R\sqrt 3 \).
b) Vì \(I\) là trung điểm của \(AC \Rightarrow OI \bot AC\) (quan hệ vuông góc giữa đường kính và dây cung).
Xét \(\Delta OAC\) có \(OI\) là trung tuyến đồng thời là đường cao \( \Rightarrow \Delta OAC\) cân tại \(O \Rightarrow OI\) là phân giác của \(\angle AOC\) hay \(OM\) là phân giác của \(\angle AOC\).
Ta có \(OM\) là trung trực của AC (Trong tam giác cân, đường cao đồng thời là trung trực).
Vì \(M\) thuộc trung trực của \(AC\) nên \(MA = MC \Rightarrow \Delta MAC\) cân tại \(M\).
\( \Rightarrow \angle MAC = \angle MCA\,\,\left( 1 \right)\)
\(\Delta OAC\) cân tại \(O \Rightarrow \angle OAC = \angle OCA\) (2)
Từ (1) và (2) \( \Rightarrow \angle MCA + \angle OCA = \angle MAC + \angle OAC \)
\(\Rightarrow \angle OCM = \angle OAM = {90^0}\).
\( \Rightarrow MC \bot OC\) tại \(C\). Mà \(OC\) là bán kính của \(\left( O \right)\).
Vậy \(MC\) là tiếp tuyến của \(\left( O \right)\).
c) Áp dụng tính chất hai tiếp tuyến cắt nhau ta có:
\(\left\{ \begin{array}{l}MC = MA\\NC = NB\end{array} \right.\)
\(\Rightarrow MN = MC + NC = AM + BN\)
Ta có : OM là tia phân giác của \(\angle AOC\), ON là tia phân giác của \(\angle BOC\) (tính chất 2 tiếp tuyến cắt nhau).
Mà \(\angle AOC\) và \(\angle BOC\) là hai góc kề bù \( \Rightarrow OM \bot ON \Rightarrow \angle MON = {90^0}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 10 trang 146 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







