Bài 12 trang 146 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho đường tròn (O). Từ một điểm M ở ngoài (O),
Đề bài
Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất 2 tiếp tuyến cắt nhau và dựa vào giả thiết, chứng minh tam giác MAB đều.
Lời giải chi tiết
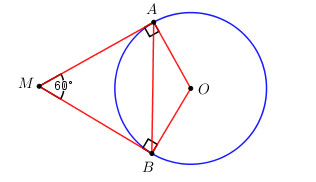
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có \(MA = MB\).
Xét \(\Delta MAB\) có: \(\left\{ \begin{array}{l}MA = MB\,\,\left( {cmt} \right)\\\angle AMB = {60^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta MAB\) đều \( \Rightarrow AB = MA = MB\).
\( \Rightarrow \) Chu vi tam giác \(ABC\) là : \({C_{ABC}} = AB + MA + MB \)\(\,= 3AB = 18\)
\(\Leftrightarrow AB = 6\,\,\left( {cm} \right)\).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 12 trang 146 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 12 trang 146 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







