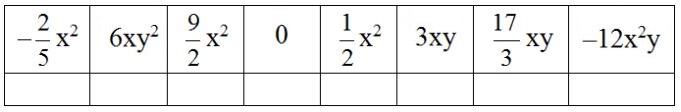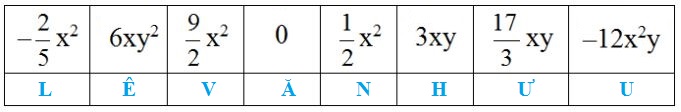Bài 18 trang 35 SGK Toán 7 tập 2

Đề bài

Đố:

Tên của tác giả cuốn Đại Việt sử kí dưới thời vua Trần Nhân Tông được đặt cho một đường phố của Thủ đô Hà Nội. Em sẽ biết tên tác giả đó bằng cách tính tổng và hiệu dưới đây rồi viết chữ tương ứng vào ô dưới kết quả được cho trong bảng sau:

V  \(2{x^2} + 3{x^2} - \dfrac{1}{2}{x^2}\);

N   \( - \dfrac{1}{2}{x^2} + {x^2}\);

H   \(  xy - 3xy + 5xy\); 

Ă   \(7{y^2}{z^3} + ( - 7{y^2}{z^3})\);

Ư   \(5xy -\dfrac{1}{3} xy + xy\);

U   \( - 6{x^2}y-6{x^2}y\);

Ê    \(3x{y^2} - ( - 3x{y^2})\);

L    \(- \dfrac{1}{5}{x^2} + \left( { - \dfrac{1}{5}{x^2}} \right)\);

Lời giải chi tiết

Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng. 

V  \(2{x^2} + 3{x^2} - \dfrac{1}{2}{x^2} = \left( {2 + 3 - \dfrac{1}{2}} \right){x^2} \)\(\,= \left( {\dfrac{4}{2} + \dfrac{6}{2} - \dfrac{1}{2}} \right){x^2} = \dfrac{9}{2}{x^2}\)

N  \( - \dfrac{1}{2}{x^2} + {x^2} = \left( { - \dfrac{1}{2} + 1} \right){x^2} \)\(\,= \left( { - \dfrac{1}{2} + \dfrac{2}{2}} \right){x^2} = \dfrac{1}{2}{x^2}\) 

H  \(xy - 3xy + 5xy = \left( {1 - 3 + 5} \right)xy\)\(\, = 3xy\);

Ă  \(7{y^2}{z^3} + ( - 7{y^2}{z^3}) = \left[ {7 + \left( { - 7} \right)} \right]{y^2}{z^3} \)\(\,= 0\);

Ư  \(5xy - \dfrac{1}{3}xy + xy = \left( {5 - \dfrac{1}{3} + 1} \right)xy\)\(\, = \left( {\dfrac{{15}}{3} - \dfrac{1}{3} + \dfrac{3}{3}} \right)xy = \dfrac{{17}}{3}xy\)

U  \( - 6{x^2}y - 6{x^2}y = \left[ {\left( { - 6} \right) - 6} \right]{x^2}y \)\(\,=  - 12{x^2}y\)

Ê  \(3x{y^2} - ( - 3x{y^2}) = 3x{y^2} + 3x{y^2} \)\(\,= \left( {3 + 3} \right)x{y^2} = 6x{y^2}\)

L  \( - \dfrac{1}{5}{x^2} + \left( { - \dfrac{1}{5}{x^2}} \right) \)\(\,= \left[ {\left( { - \dfrac{1}{5}} \right) + \left( { - \dfrac{1}{5}} \right)} \right]{x^2}\)\(\, = \dfrac{{ - 2}}{5}{x^2}\)

Ta có bảng kết quả sau:

Vậy tên của tác giả cuốn Đại Việt sử kí là Lê Văn Hưu.